题目内容
如图,已知抛物线![]() :
:![]() 和⊙
和⊙![]() :
:![]() ,过抛物线
,过抛物线![]() 上一点
上一点
![]() 作两条直线与⊙
作两条直线与⊙![]() 相切于
相切于![]() 、
、![]() 两点,分别交抛物线为E、F两点,圆心点
两点,分别交抛物线为E、F两点,圆心点![]() 到抛物线准线的距离为
到抛物线准线的距离为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)当![]() 的角平分线垂直
的角平分线垂直![]() 轴时,求直线
轴时,求直线![]() 的斜率.
的斜率.

解:(I)依题意,以![]() 的中点
的中点![]() 为原点建立直角坐标系
为原点建立直角坐标系![]() (如图),
(如图),
 则点
则点![]() 的横坐标为
的横坐标为![]() .点
.点![]() 的纵坐标
的纵坐标![]() 满足方程
满足方程![]() ,
,
解得![]()
所以![]()
![]() ,其定义域为
,其定义域为![]()
(II)记![]() , 则
, 则![]() .
.
令![]() ,得
,得![]() .因为当
.因为当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上是单调递增函数,在
上是单调递增函数,在![]() 上是单调递减函数,
上是单调递减函数,
所以![]() 是
是![]() 的最大值.
的最大值.
因此,当![]() 时,
时,![]() 也取得最大值,最大值为
也取得最大值,最大值为![]() .
.

练习册系列答案
相关题目
 :
: 和⊙
和⊙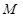 :
: ,过抛物线
,过抛物线 作两条直线与⊙
作两条直线与⊙ 相切于
相切于 、
、 两点,分别交抛物线为E、F两点,圆心点
两点,分别交抛物线为E、F两点,圆心点 .
.
 的方程;
的方程; 的角平分线垂直
的角平分线垂直 轴时,求直线
轴时,求直线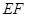 的斜率;
的斜率; 在
在 轴上的截距为,求的最小值.
轴上的截距为,求的最小值. :
: 和⊙
和⊙ :
: ,过抛物线
,过抛物线 作两条直线与⊙
作两条直线与⊙ 、
、 两点,分别交抛物线为E、F两点,圆心点
两点,分别交抛物线为E、F两点,圆心点 .
.
 的角平分线垂直轴时,求直线
的角平分线垂直轴时,求直线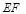 的斜率;
的斜率; 在
在 轴上的截距为,求的最小值.
轴上的截距为,求的最小值. :
: 和⊙
和⊙ :
: ,过抛物线
,过抛物线 作两条直线与⊙
作两条直线与⊙ 相切于
相切于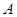 、
、 两点,分别交抛物线为E、F两点,圆心点
两点,分别交抛物线为E、F两点,圆心点 .
.
 的方程;
的方程; 的角平分线垂直
的角平分线垂直 轴时,求直线
轴时,求直线 的斜率;
的斜率; 在
在 轴上的截距为,求的最小值.
轴上的截距为,求的最小值. :
: 和⊙
和⊙ :
: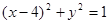 ,过抛物线
,过抛物线 作两条直线与⊙
作两条直线与⊙ 、
、 两点,分别交抛物线于
两点,分别交抛物线于 两点,圆心点
两点,圆心点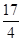 .
.
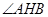 的角平分线垂直
的角平分线垂直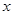 轴时,求直线
轴时,求直线 的斜率;
的斜率; 在
在 轴上的截距为
轴上的截距为 ,求
,求