题目内容
已知圆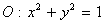 和点
和点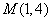 .
.
(1)过点M向圆O引切线,求切线的方程;
(2)求以点M为圆心,且被直线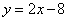 截得的弦长为8的圆M的方程;
截得的弦长为8的圆M的方程;
(3)设P为(2)中圆M上任意一点,过点P向圆O引切线,切点为Q,试探究:平面内是否存在一定点R,使得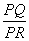 为定值?若存在,请求出定点R的坐标,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请求出定点R的坐标,并指出相应的定值;若不存在,请说明理由.
解:(1)若过点M的直线斜率不存在,直线方程为: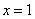 ,为圆O的切线; …………1分
,为圆O的切线; …………1分
当切线l的斜率存在时,设直线方程为: ,即
,即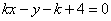 ,
,
∴圆心O到切线的距离为: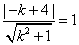 ,解得:
,解得: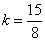
∴直线方程为: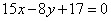 .
.
综上,切线的方程为: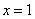 或
或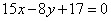 ……………4分
……………4分
(2)点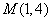 到直线
到直线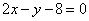 的距离为:
的距离为: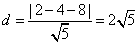 ,
,
又∵圆被直线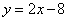 截得的弦长为8 ∴
截得的弦长为8 ∴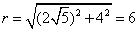 ……………7分
……………7分
∴圆M的方程为: ……………8分
……………8分
(3)假设存在定点R,使得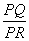 为定值,设
为定值,设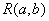 ,
,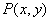 ,
,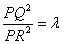
∵点P在圆M上 ∴ ,则
,则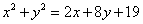 ……………10分
……………10分
∵PQ为圆O的切线∴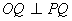 ∴
∴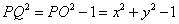 ,
,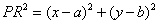
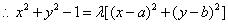 即
即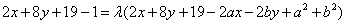
整理得: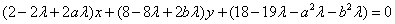 (*)
(*)
若使(*)对任意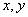 恒成立,则
恒成立,则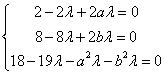 ……………13分
……………13分
∴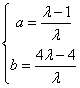 ,代入得:
,代入得: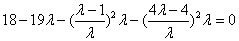
整理得: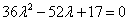 ,解得:
,解得: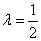 或
或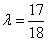 ∴
∴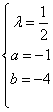 或
或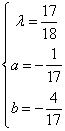
∴存在定点R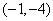 ,此时
,此时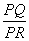 为定值
为定值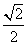 或定点R
或定点R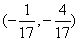 ,此时
,此时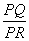 为定值
为定值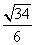 .
.
………………16分

练习册系列答案
相关题目

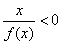 的解集为( )
的解集为( ) ,则
,则 的最大值为 .
的最大值为 . 成等差数列,过点
成等差数列,过点 作直线
作直线 的垂线,垂足为
的垂线,垂足为 .又已知点
.又已知点 ,则线段
,则线段 长的取值范围是 .
长的取值范围是 .

 ,则此数列前30项和等于( )
,则此数列前30项和等于( )
 小正周期为
小正周期为 ,且图象关于直线
,且图象关于直线 对称的是 ( )
对称的是 ( ) B.
B. C.
C. D.
D.