Question

【题目】若数列是公差为2的等差数列，数列满足，且.

(1)求数列,的通项公式；

(2)设数列{cn}满足，数列{cn}的前n项和为Tn，若不等式 对一切n∈N*恒成立，求实数λ的取值范围.

Answer 1

【答案】（1）， ；（2）

【解析】试题分析：

（1）由递推关系可得，由等差数列通项公式可得，且数列满足，数列是等比数列，其通项公式为．

（2）结合(1)的结论错位相减可得，结合恒成立的条件分类讨论n为奇数偶数两种情况可得实数的取值范围是．

试题解析：

（1）∵数列满足， ，且，∴，解得，

又数列是公差为2的等差数列，∴，

∴，化为，

∴数列是等比数列，公比为2，∴．

（2）设数列满足，

数列的前项和为，

∴，

∴，

∴，

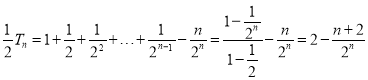不等式，化为： ，

时， ，∴；

时， ，∴，

综上可得：实数的取值范围是．