题目内容
如图所示,在正方体ABCD—A1B1C1D1中,E,F分别是BB1,CD的中点.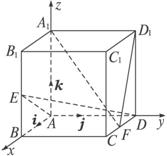
(1)求证:AD⊥D1F;
(2)求AE与D1F所成角的大小;
(3)求证:平面AED⊥平面A1FD1.
解:设正方体的棱长为1,且设![]() =i,
=i, ![]() =j,
=j,![]() =k,建立空间直角坐标系A—xyz.如右图,
=k,建立空间直角坐标系A—xyz.如右图,

(1)因为D(0,1,0),F(![]() ,1,0),D1(0,1,1),
,1,0),D1(0,1,1),
所以![]() =(0,1,0),
=(0,1,0),![]() =(
=(![]() ,0,-1).
,0,-1).
所以![]()
![]() =0+0+0=0.
=0+0+0=0.
所以![]() ⊥
⊥![]() .
.
所以AD⊥D1F.
(2)因为E(1,0,![]() ),
),
所以![]() =(1,0,
=(1,0,![]() ).
).
所以![]() ·
·![]() =
=![]() -
-![]() =0.
=0.
所以![]() ⊥
⊥![]() ,
,
所以AE与D1F所成角为90°.
(3)因为![]() ·
·![]() =(0,1,0)·(
=(0,1,0)·(![]() ,0,-1)=0,
,0,-1)=0,
所以AD⊥D1F.
所以AD⊥D1F.
又因为AE⊥D1F,AD∩AE=A,
所以D1F⊥平面AED,又D1F![]() 平面A1FD1,
平面A1FD1,
所以平面AED⊥平面A1FD1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
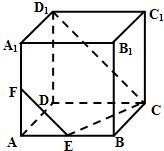 如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点
如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点
 (2011•宝山区二模)如图所示,在正方体ABCD-A1B1C1D1的侧面ABB1A1内有一动点P到直线A1B1和直线BC的距离相等,则动点P所在曲线形状为( )
(2011•宝山区二模)如图所示,在正方体ABCD-A1B1C1D1的侧面ABB1A1内有一动点P到直线A1B1和直线BC的距离相等,则动点P所在曲线形状为( ) 如图所示,在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到直线A1B1与直线BC的距离相等,则动点P所在曲线的形状为( )
如图所示,在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到直线A1B1与直线BC的距离相等,则动点P所在曲线的形状为( )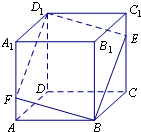 如图所示,在正方体ABCD-A1B1C1D1中,点E是棱CC1上的一个动点,平面BED1交棱AA1于点F.则下列命题中假命题是( )
如图所示,在正方体ABCD-A1B1C1D1中,点E是棱CC1上的一个动点,平面BED1交棱AA1于点F.则下列命题中假命题是( )