题目内容
已知函数 ,若f(x)>kx对任意的x∈R恒成立,则k的取值范围是________.
,若f(x)>kx对任意的x∈R恒成立,则k的取值范围是________.
(-2,0]
分析:转化函数f(x)的最值问题解决,分x≤0,x>0两种情况讨论可得f(x)的最值.
解答:当x≤0时,f(x)>kx,即x2+1>kx,x=0时k∈R;
当x<0时,有x+ <k,而x+
<k,而x+ -2(x=-1取等号),所以k>-2;
-2(x=-1取等号),所以k>-2;
故x≤0时,f(x)>kx恒成立,得k>-2;
当x>0时,f(x)>kx,即为ln(x+1)>kx,而ln(x+1)>0,
结合图象可知,要使该不等式恒成立,只需k≤0;
综上,要使f(x)>kx对任意的x∈R恒成立,k的范围为-2<k≤0.
故答案为:(-2,0]
点评:本题考查函数恒成立问题,考查分类讨论思想,考查学生分析解决问题的能力.
分析:转化函数f(x)的最值问题解决,分x≤0,x>0两种情况讨论可得f(x)的最值.
解答:当x≤0时,f(x)>kx,即x2+1>kx,x=0时k∈R;
当x<0时,有x+
 <k,而x+
<k,而x+ -2(x=-1取等号),所以k>-2;
-2(x=-1取等号),所以k>-2;故x≤0时,f(x)>kx恒成立,得k>-2;
当x>0时,f(x)>kx,即为ln(x+1)>kx,而ln(x+1)>0,
结合图象可知,要使该不等式恒成立,只需k≤0;
综上,要使f(x)>kx对任意的x∈R恒成立,k的范围为-2<k≤0.
故答案为:(-2,0]
点评:本题考查函数恒成立问题,考查分类讨论思想,考查学生分析解决问题的能力.

练习册系列答案
相关题目
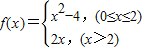 ,若f(x)=12,则x= .
,若f(x)=12,则x= .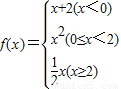 ,若f(x)=2,则x的值为( )
,若f(x)=2,则x的值为( )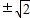
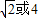
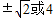
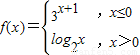 ,若f(x)≥1,则x的取值范围为 .
,若f(x)≥1,则x的取值范围为 .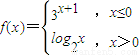 ,若f(x)≥1,则x的取值范围为 .
,若f(x)≥1,则x的取值范围为 .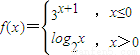 ,若f(x)≥1,则x的取值范围为 .
,若f(x)≥1,则x的取值范围为 .