题目内容
把函数y=-3cos(2x+
)的图象向右平移m(m>0)个单位,设所得图象的解析式为y=f(x),则当y=f(x)是偶函数时,m的值可以是( )
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:根据函数的图象的平移法则先求得y=f(x)=-3cos(2x+
π-2m)由y=f(x)是偶函数时,根据偶函数的性质可得,在对称轴y轴处将取得函数的最值可得f(0)=±3,解出m,结合选项可求
| 1 |
| 3 |
解答:解:把函数y=-3cos(2x+
)的图象向右平移m(m>0)个单位,
所得图象的解析式为y=f(x)=-3cos(2x+
π-2m)
当y=f(x)是偶函数时,根据偶函数的性质可得,在对称轴y轴处将取得函数的最值
∴f(0)=-3cos(-2m+
)=±3即-2m+
=kπ,k∈Z
则-m=
-
,k∈Z结合选项可得,当k=0时,m=
故选B
| π |
| 3 |
所得图象的解析式为y=f(x)=-3cos(2x+
| 1 |
| 3 |
当y=f(x)是偶函数时,根据偶函数的性质可得,在对称轴y轴处将取得函数的最值
∴f(0)=-3cos(-2m+
| π |
| 3 |
| π |
| 3 |
则-m=
| kπ |
| 2 |
| π |
| 6 |
| π |
| 6 |
故选B
点评:本题主要考查了函数的图象的平移法则:左加右减,要注意所要加(或减)的量是在x上,这也是平常考生的容易出现错误的地方.还考查了偶函数的性质(在对称轴y轴处将取得函数的最值)的应用,灵活应用该性质可以简化运算.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
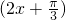 的图象向右平移m(m>0)个单位,设所得图象的解析式为y=f(x),则当y=f(x)是偶函数时,m的值可以是
的图象向右平移m(m>0)个单位,设所得图象的解析式为y=f(x),则当y=f(x)是偶函数时,m的值可以是



 的图象向右平移m(m>0)个单位,设所得图象的解析式为y=f(x),则当y=f(x)是偶函数时,m的值可以是( )
的图象向右平移m(m>0)个单位,设所得图象的解析式为y=f(x),则当y=f(x)是偶函数时,m的值可以是( )


