题目内容
已知平行六面体ABCD-A1B1C1D1的AB=5,AD=3,AA1=7,∠BAD=60°,∠BAA1=∠DAA1=90°,则AC1的长是
7
| 2 |
7
.| 2 |
分析:先利用余弦定理求AC,再证明侧棱垂直于底面,从而可求体对角线长.
解答:解:由题意,AC2=32+52-2×3×5×cos120°=49
∵∠BAA1=∠DAA1=90°,
∴侧棱垂直于底面
∴AC12=49+49=98
∴AC1的长是7
故答案为7
∵∠BAA1=∠DAA1=90°,
∴侧棱垂直于底面
∴AC12=49+49=98
∴AC1的长是7
| 2 |
故答案为7
| 2 |
点评:本题主要考查了体对角线的求解,以及余弦定理的应用,同时考查了空间想象能力,计算推理的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.
如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O. 如图,已知平行六面体ABCD-A1B1C1D1.
如图,已知平行六面体ABCD-A1B1C1D1.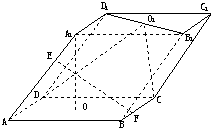 如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.
如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O. 如图,已知平行六面体ABCD-A1B1C1D1.
如图,已知平行六面体ABCD-A1B1C1D1.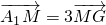 ,设
,设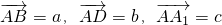 ,用向量a、b、c表示向量
,用向量a、b、c表示向量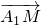 ;
;