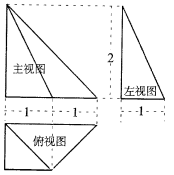
题目内容
如图, 是半圆
是半圆 的直径,
的直径, 是半圆
是半圆 上除
上除 、
、 外的一个动点,
外的一个动点, 平面
平面 ,
, ,
, ,
, ,
, .
.

⑴证明:平面 平面
平面 ;
;
⑵试探究当 在什么位置时三棱锥
在什么位置时三棱锥 的体积取得最大值,请说明理由并求出这个最大值.
的体积取得最大值,请说明理由并求出这个最大值.
 是半圆
是半圆 的直径,
的直径, 是半圆
是半圆 上除
上除 、
、 外的一个动点,
外的一个动点, 平面
平面 ,
, ,
, ,
, ,
, .
.
⑴证明:平面
 平面
平面 ;
;⑵试探究当
 在什么位置时三棱锥
在什么位置时三棱锥 的体积取得最大值,请说明理由并求出这个最大值.
的体积取得最大值,请说明理由并求出这个最大值.⑴ 是直径,所以
是直径,所以 ,因为
,因为 平面
平面 ,
, ,所以
,所以 平面
平面 因为
因为 ,又因为
,又因为 ,所以
,所以 ,所以
,所以 平面ACD,因为
平面ACD,因为 平面
平面 ,所以平面
,所以平面 平面
平面
⑵当 为半圆弧中点时三棱锥
为半圆弧中点时三棱锥 的体积取得最大值,最大值为
的体积取得最大值,最大值为
 是直径,所以
是直径,所以 ,因为
,因为 平面
平面 ,
, ,所以
,所以 平面
平面 因为
因为 ,又因为
,又因为 ,所以
,所以 ,所以
,所以 平面ACD,因为
平面ACD,因为 平面
平面 ,所以平面
,所以平面 平面
平面
⑵当
 为半圆弧中点时三棱锥
为半圆弧中点时三棱锥 的体积取得最大值,最大值为
的体积取得最大值,最大值为
试题分析:⑴因为
 是直径,所以
是直径,所以 ,因为
,因为 平面
平面 ,
, ,因为
,因为 ,所以
,所以 平面
平面
因为
 ,又因为
,又因为 ,所以四边形
,所以四边形 是平行四边形,所以
是平行四边形,所以 ,所以
,所以 平面,因为
平面,因为 平面
平面 ,所以平面
,所以平面 平面
平面
⑵依题意,
 ,
,由⑴知

 ,
, ,
, ,等号当且仅当
,等号当且仅当 时成立,所以当
时成立,所以当 为半圆弧中点时三棱锥
为半圆弧中点时三棱锥 的
的体积取得最大值,最大值为

(备注:此时,
 ,
, ,设三棱锥
,设三棱锥 的高为
的高为 ,则
,则 ,
, ).
).点评:第一问要证明两面垂直只需证明其中一个平面内的一条直线垂直于另外一面,即转化为证明线面垂直;第二问首先采用等体积法将所求椎体的体积转化求解的角度,而后借助于均值不等式求得最大值

练习册系列答案
相关题目
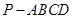 中,
中,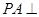 底面
底面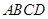 ,四边形
,四边形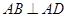 ,
,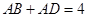 ,
,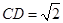 ,
,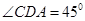 .
.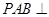 平面
平面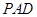 ;
;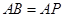 .
.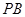 与平面
与平面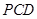 所成的角为
所成的角为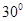 ,求线段
,求线段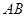 的长;
的长;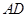 上是否存在一个点
上是否存在一个点 ,使得点
,使得点 的距离都相等?说明理由.
的距离都相等?说明理由.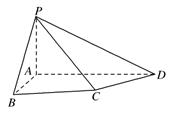
 的底面是菱形,且
的底面是菱形,且 面
面 ,
, ,
, ,
, 为棱
为棱 的中点,
的中点, 为线段
为线段 的中点,
的中点,
 面
面 与平面
与平面 的位置关系,并证明你的结论;
的位置关系,并证明你的结论; 的体积.
的体积. 中,平面
中,平面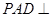 平面
平面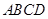 ,
,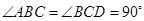 ,
,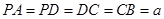 ,
,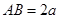 ,
,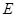 是
是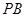 中点,
中点,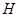 是
是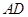 中点.
中点. 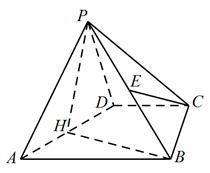
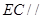 平面
平面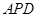 ;
;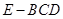 的体积.
的体积.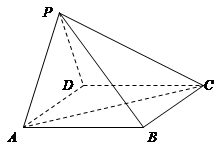
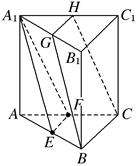
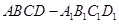 的棱线长为1,面对角线
的棱线长为1,面对角线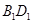 上有两个动点E,F,且
上有两个动点E,F,且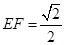 ,则下列四个结论中①
,则下列四个结论中①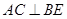 ②
②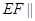 平面
平面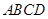 ③三棱锥
③三棱锥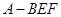 的体积为定值 ④异面直线
的体积为定值 ④异面直线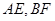 所成的角为定值,其中正确的个数是
所成的角为定值,其中正确的个数是