题目内容
15.函数f(x)=$\left\{\begin{array}{l}a{x^2}+x-1(x>2)\\ ax-1(x≤2)\end{array}$是R上的单调递减函数,则实数a的取值范围是( )| A. | -$\frac{1}{4}$≤a<0 | B. | a≤-$\frac{1}{4}$ | C. | -1≤a≤-$\frac{1}{4}$ | D. | a≤-1 |
分析 根据条件f(x)在R上单调递减,从而f(x)=ax2+x-1在(2,+∞)上单调递减,根据二次函数的单调性便有$\left\{\begin{array}{l}{a<0}\\{-\frac{1}{2a}≤2}\end{array}\right.$,这样可解出a$≤-\frac{1}{4}$,根据一次函数的单调性有a<0.根据减函数的定义可得到,a•22+2-1≤a•2-1,这又可得到一个a的范围,然后这几个a的范围求交集即可得出实数a的取值范围.
解答 解:①x>2时,f(x)=ax2+x-1;
f(x)在(2,+∞)上单调递减;
∴$\left\{\begin{array}{l}{a<0}\\{-\frac{1}{2a}≤2}\end{array}\right.$;
∴$a≤-\frac{1}{4}$;
②x≤2时,f(x)=ax-1单调递减;
∴a<0;
又f(x)在R上单调递减;
∴a•22+2-1≤a•2-1;
∴a≤-1;
∴综上得实数a的取值范围为(-∞,-1].
故选:D.
点评 考查二次函数的开口方向和对称轴,二次函数的单调性,一次函数的单调性,以及减函数的定义,分段函数单调性的特点.

练习册系列答案
相关题目
2.下列各式中,正确的是( )
| A. | 2⊆{x|x≤2} | B. | {2}⊆{x|x<2} | C. | 2∈{x|x≤2} | D. | ∅∈{x|x≤2} |
3.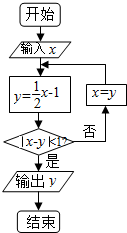 执行如图所示的程序框图,若输入x的值为4,则输出的结果是( )
执行如图所示的程序框图,若输入x的值为4,则输出的结果是( )
 执行如图所示的程序框图,若输入x的值为4,则输出的结果是( )
执行如图所示的程序框图,若输入x的值为4,则输出的结果是( )| A. | 1 | B. | $-\frac{1}{2}$ | C. | $-\frac{5}{4}$ | D. | $-\frac{13}{8}$ |
4.直线l:mx-y+3-m=0与圆C:x2+(y-1)2=5的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 有公共点 |
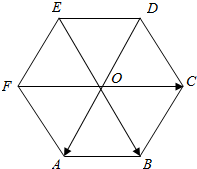 如图所示.O是正六边形ABCDEF的中心,且$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,$\overrightarrow{OC}=\overrightarrow{c}$.
如图所示.O是正六边形ABCDEF的中心,且$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,$\overrightarrow{OC}=\overrightarrow{c}$.