题目内容
在
中，
分别为角
的对边，的面积S满足
(Ⅰ)求角A的值;
(Ⅱ)若
,设角B的大小为x,用x表示c,并求c的取值范围.
中，分别为角的对边，的面积S满足(Ⅰ)求角A的值;
(Ⅱ)若
,设角B的大小为x,用x表示c,并求c的取值范围.(Ⅰ)
；(Ⅱ) 
.
；(Ⅱ) .试题分析：(Ⅰ) 因为已知
，又因为三角形的面积的可表示为
.解得
.所以 .本题掌握三角形的面积公式
的形式是关键.(Ⅱ)由于
，
.所以
.又因为已知.所以利用正弦定理可求出边c关于x的表达式.再根据角的范围求出正弦值的范围即为边长c的范围，最后面是易错点.试题解析：（1）在
中，由
，得∵
∴ 5分（2）由
及正弦定理得：
，∴
∵
∴
∴
∴
，
，即
12分
练习册系列答案
能力评价系列答案
相关题目
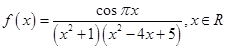，给出下列四个命题:
是周期函数，
，函数
。
（其中
）的部分图象如图所示．
的解析式；
的解集．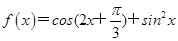
.
的单调递减区间及最小正周期；
若
，
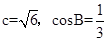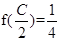，求
对x∈R恒成立，且
<f(π)，则下列结论正确的是( )．
＝－1
>f
(k∈Z)
,若
,则方程
在
内的所有实数根之和为 .
在一个周期内的图像如图，此函数的解析式为（ ）
的最小正周期是 .
的最小正周期为
,最大值为
,则（ ）
,
,