题目内容
已知a、b为正有理数,设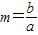 ,
,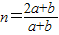 .
.(Ⅰ)比较m、n的大小;
(Ⅱ)求证:
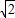 的大小在m、n之间.
的大小在m、n之间.
【答案】分析:(Ⅰ)将m、n作差后变形到因式乘积的形式,分类讨论此差与零的关系,从而得出它们的大小关系.
(Ⅱ)先求出m- 与 m+
与 m+ 的解析式,考查(m-
的解析式,考查(m- )与 (m+
)与 (m+ )的积的符号小于零,故
)的积的符号小于零,故 的大小在m、n之间.
的大小在m、n之间.
解答:解:(Ⅰ) ,
,
∵a、b为正有理数,∴ ,
,
∴当 时,m>n,当
时,m>n,当 时,m<n.
时,m<n.
(Ⅱ)∵ ,
, ,
,
∴ ,
,
因此, 的大小在m、n之间.
的大小在m、n之间.
点评:本题考查不等式的基本性质,体现了分类讨论的数学思想;证明 的大小在m、n之间,只要证明 (m-
的大小在m、n之间,只要证明 (m- )与 (m+
)与 (m+ )的积的符号小于零即可.
)的积的符号小于零即可.
(Ⅱ)先求出m-
 与 m+
与 m+ 的解析式,考查(m-
的解析式,考查(m- )与 (m+
)与 (m+ )的积的符号小于零,故
)的积的符号小于零,故 的大小在m、n之间.
的大小在m、n之间.解答:解:(Ⅰ)
 ,
,∵a、b为正有理数,∴
 ,
,∴当
 时,m>n,当
时,m>n,当 时,m<n.
时,m<n.(Ⅱ)∵
 ,
, ,
,∴
 ,
,因此,
 的大小在m、n之间.
的大小在m、n之间.点评:本题考查不等式的基本性质,体现了分类讨论的数学思想;证明
 的大小在m、n之间,只要证明 (m-
的大小在m、n之间,只要证明 (m- )与 (m+
)与 (m+ )的积的符号小于零即可.
)的积的符号小于零即可. 
练习册系列答案
相关题目
 ,
, .
. 的大小在m、n之间.
的大小在m、n之间.