题目内容
在等差数列{an}中,a2=4,a6=12,,那么数列{ }的前n项和等于( )
}的前n项和等于( )A.

B.

C.

D.

【答案】分析:求出等差数列的通项,要求的和是一个等差数列与一个等比数列的积构成的数列,利用错位相减法求出数列的前n项的和.
解答:解:∵等差数列{an}中,a2=4,a6=12;
∴公差d=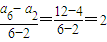 ;
;
∴an=a2+(n-2)×2=2n;
∴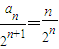 ;
;
∴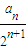 的前n项和,
的前n项和,
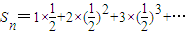
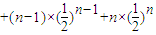
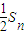 =
=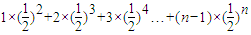
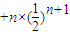
两式相减得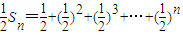
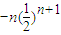
=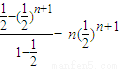
∴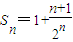
故选B
点评:求数列的前n项的和,先判断通项的特点,据通项的特点选择合适的求和方法.
解答:解:∵等差数列{an}中,a2=4,a6=12;
∴公差d=
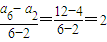 ;
;∴an=a2+(n-2)×2=2n;
∴
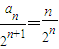 ;
;∴
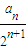 的前n项和,
的前n项和,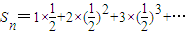
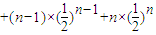
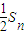 =
=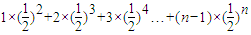
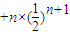
两式相减得
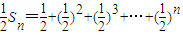
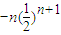
=
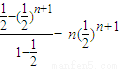
∴
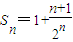
故选B
点评:求数列的前n项的和,先判断通项的特点,据通项的特点选择合适的求和方法.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目