题目内容
抛物线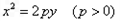 过焦点F的直线l交抛物线于A.B两点,O为原点,若△AOB面积最小值为8。
过焦点F的直线l交抛物线于A.B两点,O为原点,若△AOB面积最小值为8。
(1)求P值
(2)过A点作抛物线的切线交y轴于N,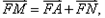 则点M在一定直线上,试证明之。
则点M在一定直线上,试证明之。
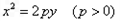 过焦点F的直线l交抛物线于A.B两点,O为原点,若△AOB面积最小值为8。
过焦点F的直线l交抛物线于A.B两点,O为原点,若△AOB面积最小值为8。 (1)求P值
(2)过A点作抛物线的切线交y轴于N,
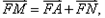 则点M在一定直线上,试证明之。
则点M在一定直线上,试证明之。⑴∵抛物线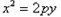 的焦点
的焦点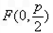
∴设直线l方程为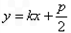
由 消去y得
消去y得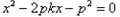
设
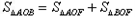
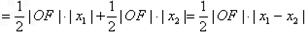
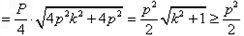
当k=0的等号成立
∴S△AOB面积的最小值为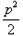
∴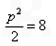
∵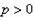 ∴p=4
∴p=4
⑵∵x2=8y∴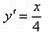
∴过A点的切线方程为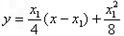 即
即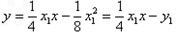
∴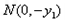
设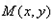 ,又∵
,又∵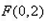 ∴
∴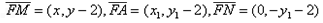
∵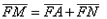 ∴
∴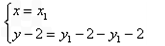
得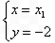 ∴M点在直线
∴M点在直线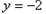 上
上

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 设抛物线M方程为y2=2px(p>0),其焦点为F,P(a,b)(a≠0)为直线y=x与抛物线M的一个交点,|PF|=5
设抛物线M方程为y2=2px(p>0),其焦点为F,P(a,b)(a≠0)为直线y=x与抛物线M的一个交点,|PF|=5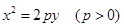 过焦点F的直线
过焦点F的直线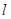 交抛物线于A、B两点,O为原点,若
交抛物线于A、B两点,O为原点,若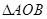 面积最小值为8。
面积最小值为8。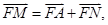 则点M在一定直线上,试证明之。
则点M在一定直线上,试证明之。