题目内容
若O是△ABC内一点,
+
+
=
,则O是△ABC的( )
| OA |
| OB |
| OC |
| 0 |
| A、内心 | B、外心 | C、垂心 | D、重心 |
分析:利用向量的运算法则:平行四边形法则得到A,O,D共线且O为三角形中线的三等分点,据三角形重心的性质判断出O为重心.
解答:解:以
、
为邻边作平行四边形OBDC,
则
=
+
.
又
+
+
=
,
∴
+
=-
.
∴-
=
.
∴O为AD的中点,且A、O、D共线.
又E为OD的中点,
∴O是中线AE的三等分点,且OA=
AE.
∴O是△ABC的重心.
故选D
| OB |
| OC |
则
| OD |
| OB |
| OC |
又
| OA |
| OB |
| OC |
| 0 |
∴
| OB |
| OC |
| OA |
∴-
| OA |
| OD |
∴O为AD的中点,且A、O、D共线.
又E为OD的中点,
∴O是中线AE的三等分点,且OA=
| 2 |
| 3 |
∴O是△ABC的重心.
故选D
点评:本题考查向量的运算法则:平行四边形法则、考查三角形的重心的性质:分三角形的中线为2:1的关系.

练习册系列答案
相关题目
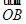 |·
|·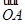 +|
+| .将它类比到平面的情形是:若O是△ABC内一点,有S△OBC·
.将它类比到平面的情形是:若O是△ABC内一点,有S△OBC· =
=