Question

已知函数f(x)=,x∈［0,1］.

(1)求f(x)的单调区间和值域;

(2)设a≥1,函数g(x)=x³-3a²x-2a,x∈［0,1］,若对于任意x₁∈［0,1］,总存在x₀∈［0,1］,使得g(x₀)=f(x₁)成立,求a的取值范围.

Answer 1

解:(1)对函数f(x)求导,得f′(x)==-,

    令f′(x)=0解得x=或x=.当x变化时,f′(x)、f(x)的变化情况如下表:

x	0	(0,)		(,1)	1
f′(x)		-	0	+
f(x)	-	↘	-4	↗	-3

    所以,当x∈(0,)时,f(x)是减函数;

    当x∈(,1)时,f(x)是增函数;

    当x∈［0,1］时,f(x)的值域为［-4,-3］.

    (2)对函数g(x)求导,得g′(x)=3(x²-a²).

    因为a≥1,当x∈(0,1)时,g′(x)＜3(1-a²)≤0,

    因此当x∈(0,1)时,g(x)为减函数,从而当x∈［0,1］时有g(x)∈［g(1),g(0)］.

    又g(1)=1-2a-3a²,g(0)=-2a,即当x∈［0,1］时有g(x)∈［1-2a-3a²,-2a］.

    任给x₁∈［0,1］,f(x₁)∈［-4,-3］,存在x₀∈［0,1］使得g(x₀)=f(x₁),

    则［1-2a-3a²,-2a］［-4,-3］,

    即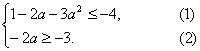

    解①式得a≥1或a≤-;

    解②式得a≤.

    又a≥1,故a的取值范围为1≤a≤.