题目内容
从某校参加初中毕业考试的学生中，抽取了30名学生的数学成绩，分数如下：90，85，84，86，87，98，79，85，90，93，68，95，85，71，78，61，94，88，77，100，70，97，85，68，99，88，85，92，93，97．
这个样本数据的频率分布表如下：
填空：(1)这个样本数据的众数是________分．
(2)列频率分布表时，所取的组距为________分．
(3)在这个频率分布表中，数据落在94.5－99.5分范围内的频数为________．
(4)在这个频率分布表中，数据落在74.5－79.5分范围内的频率为________．
(5)在这个频率分布表中，频率最大的一组数据的范围是________分．
(6)估计这个学校初中毕业考试的数学成绩在80分以上(含80分)的约占________％．
答案：
解析：
解析：
|
答案：(1)85 (2)5 (3)5 (4)0.100 (5)84.5－89.5 (6)73.3 思路解析：(1)众数：频率分布的最大值所对应的样本数据，84.5－89.5一组的频数最大为9，而其中数据85的频数为5，出现次数最多，85即是众数． (6)估计这个学校初中毕业考试的数学成绩在80分以上(含80分)的约占0.033＋0.300＋0.200＋0.167＋0.033＝0.733，即73.3％． |
练习册系列答案
相关题目
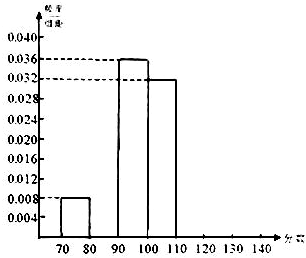从某校参加2009年全国高中数学联赛预赛的450名同学中，随机抽取若干名同学，将他们的成绩制成频率分布表，下面给出了此表中部分数据．（1）根据表中已知数据，你认为在①、②、③处的数值分别为
（2）补全在区间[70，140]上的频率分布直方图；
（3）若成绩不低于110分的同学能参加决赛，那么可以估计该校大约有多少学生能参加决赛？
| 分组 | 频数 | 频率 |
| [70，80） | 0.08 | |
| [80，90） | ③ | |
| [90，100） | 0.36 | |
| [100，110） | 16 | 0.32 |
| [110，120） | 0.08 | |
| [120，130） | 2 | ② |
| [130，140] | 0.02 | |
| 合计 | ① |
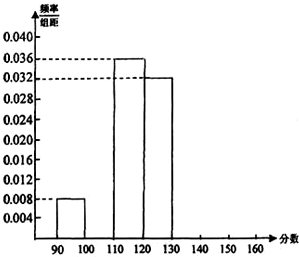从某校参加高一年级基础知识数学测试的450名同学中，随机抽取若干名同学，将他们的成绩制成如下频率分布表．（1）根据表中已知数据，填写在①、②、③处的数值分别为
（2）补全在区间[90，160]上的频率分布直方图；
（3）请你估计该校成绩不低于130分的同学人数．
| 分组 | 频数 | 频率 |
| [90，100） | 0.08 | |
| [100，110） | ② | |
| [110，120） | 0.36 | |
| [120，130） | 16 | 0.32 |
| [130，140） | 0．O8 | |
| [140，150） | 2 | ① |
| [150，160] | 0．O2 | |
| 合计 | ③ |
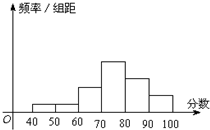从某校参加数学竞赛的试卷中抽取一个样本，考查竞赛的成绩分布，将样本分成6组，得到频率分布直方图如图，从左到右各小组的小长方形的高的比为1：1：3：6：4：2，最右边的一组的频数是8．请结合直方图的信息，解答下列问题：