题目内容
(Ⅰ)设函数
 ,求
,求 的最小值;
的最小值;(Ⅱ)设正数
 满足
满足 ,证明
,证明
(Ⅰ)解:对函数 求导数:
求导数:



于是 ,
,
当 时,
时, ,
, 在区间
在区间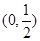 是减函数,
是减函数,
当 时,
时, ,
, 在区间
在区间 是增函数,
是增函数,
所以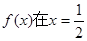 时取得最小值,
时取得最小值, ,
,
(II)用数学归纳法证明
(ⅰ)当n=1时,由(Ⅰ)知命题成立
(ⅱ)假设当n=k时命题成立
即若正数 满足
满足 ,
,
则
当n=k+1时,若正数 满足
满足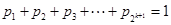 ,
,
令
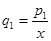 ,
, ,……,
,……,

则 为正数,且
为正数,且 ,
,
由归纳假定知

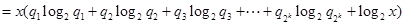

 ①
①
同理,由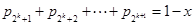 ,可得
,可得
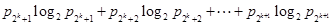
 ②
②
综合①、②两式





即当n=k+1时命题也成立
根据(ⅰ)、(ⅱ)可知对一切正整数n命题成立
 求导数:
求导数:


于是
 ,
, 当
 时,
时, ,
, 在区间
在区间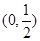 是减函数,
是减函数,当
 时,
时, ,
, 在区间
在区间 是增函数,
是增函数,所以
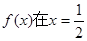 时取得最小值,
时取得最小值, ,
,(II)用数学归纳法证明

(ⅰ)当n=1时,由(Ⅰ)知命题成立

(ⅱ)假设当n=k时命题成立

即若正数
 满足
满足 ,
,则

当n=k+1时,若正数
 满足
满足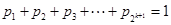 ,
,令

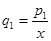 ,
, ,……,
,……,

则
 为正数,且
为正数,且 ,
,由归纳假定知


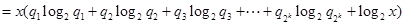

 ①
①同理,由
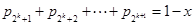 ,可得
,可得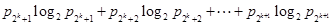
 ②
②综合①、②两式





即当n=k+1时命题也成立

根据(ⅰ)、(ⅱ)可知对一切正整数n命题成立

略

练习册系列答案
相关题目
 (Ⅱ)
(Ⅱ)
 (Ⅳ)
(Ⅳ) .
.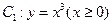 与曲线
与曲线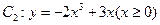 交于点
交于点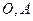 .直线
.直线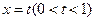 与曲线
与曲线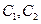 分别相交于点
分别相交于点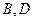 .
.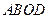 的面
的面 积
积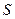 与
与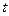 的函数关系
的函数关系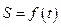 ;
;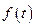 的单调性,并求
的单调性,并求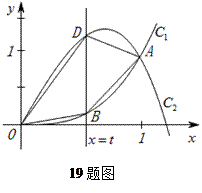
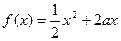 ,
,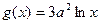 ,
,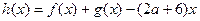 在(0,4)上为单调函数,求
在(0,4)上为单调函数,求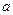 的取值范围.
的取值范围. ,若
,若 ,则
,则 ▲ ;
▲ ; 的导数为
的导数为



 在点
在点 处的切线方程为
处的切线方程为 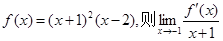 等于
等于 (x∈R),经验证:当c=1,2,3时,不等式对一切实数x都成立。试问:当c取任何正数时,不等式对任何实数x是否都成立?若能成立,请给出证明;若不成立,请求出c的取值范围,使不等式对任何实数x都能成立。
(x∈R),经验证:当c=1,2,3时,不等式对一切实数x都成立。试问:当c取任何正数时,不等式对任何实数x是否都成立?若能成立,请给出证明;若不成立,请求出c的取值范围,使不等式对任何实数x都能成立。