题目内容
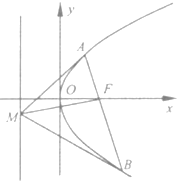 设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A(x1,y1)、B(x2,y2)
设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A(x1,y1)、B(x2,y2)(y1>0,y2<0)两点,M是抛物线的准线上的一点,O是坐标原点,若直线MA、MF、MB的斜率分别记为:kMA=a、kMF=b、kMB=c,(如图)
(1)若y1y2=-4,求抛物线的方程;
(2)当b=2时,求证:a+c为定值.
分析:(1设)直线方程为y=k(x-
)或x=
(斜率k不存在)在与抛物线方程联立,求出y1y2,再根据y1y2=-4,就可求出p值,进而求出抛物线方程.
(2)当b=2时,分别用含A,B,M三点坐标式子表示:kMA,kMF,kMB,再利用它们的关系求a+c,看是否为常数.
| p |
| 2 |
| p |
| 2 |
(2)当b=2时,分别用含A,B,M三点坐标式子表示:kMA,kMF,kMB,再利用它们的关系求a+c,看是否为常数.
解答:解:(1)设过抛物线y2=2px(p>0)的焦点F(
,0)的直线方程为y=k(x-
)或x=
(斜率k不存在),则
得
y2 -y-
=0,∴y1y2=-p2
当x=
(斜率k不存在)时,则A(
,p),B(
,-P),∴y1y2=-p2
又∵y1y2=-4∴P=2,∴所求抛物线方程为y2=4x
(2)设A(
,y1),B(
,y2),M(-
,t),F(
,0),
由已知直线MA,MF,MB的斜率分别记为:kMA,=a,kMF=b,kMB=c,
得a=
,b=
,c=
且x1=
,x2=
∴a+c=
+
=
+
=-
=2b
∵b=2,∴a+c=4∴a+c为定值.
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
|
| k |
| 2p |
| px |
| 2 |
当x=
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
又∵y1y2=-4∴P=2,∴所求抛物线方程为y2=4x
(2)设A(
| y12 |
| 2p |
| y22 |
| 2p |
| p |
| 2 |
| p |
| 2 |
由已知直线MA,MF,MB的斜率分别记为:kMA,=a,kMF=b,kMB=c,
得a=
| y1-t | ||
x1+
|
| -t |
| p |
| y2-t | ||
x2+
|
| y12 |
| 2p |
| y22 |
| 2p |
∴a+c=
| y1-t | ||
x1+
|
| y2-t | ||
x2+
|
| y1-t | ||||
|
| y2-t | ||||
|
| 2t |
| p |
∵b=2,∴a+c=4∴a+c为定值.
点评:本题主要考查了用直线与抛物线的位置关系,求抛物线方程,以及定植问题的考查,做题时应认真分析,找出联系.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
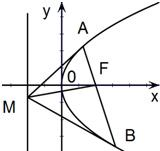 设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A,B两点,且A,B两点坐标分别为(x1,y1)、(x2,y2),y1>0,y2<0,M是抛物线的准线上的一点,O是坐标原点.若直线MA,MF,MB的斜率分别记为:KMA=a,KMF=b,KMB=c,(如图)
设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A,B两点,且A,B两点坐标分别为(x1,y1)、(x2,y2),y1>0,y2<0,M是抛物线的准线上的一点,O是坐标原点.若直线MA,MF,MB的斜率分别记为:KMA=a,KMF=b,KMB=c,(如图)