题目内容
(本小题满分12分)如图所示,在直三棱柱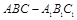 中,
中,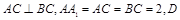 、
、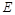 、
、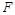 分别是
分别是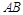 、
、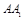 、
、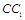 的中点,
的中点,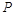 是
是 上的点.
上的点.
(1)求直线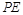 与平面
与平面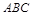 所成角的正切值的最大值;
所成角的正切值的最大值;
(2)求证:直线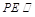 平面
平面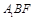 ;
;
(3)求直线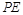 与平面
与平面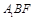 的距离.
的距离.
|
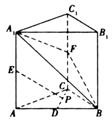
【答案】
(1)线PE与平面ABC所成角的最大值为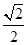
(2)略
(3)
【解析】解:(1)PE在平面ABC内的射影为AP,
则∠EPA为PE与平面ABC所成角的平面角,
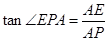
当点P与D重合时,AP最短,此时:
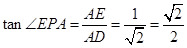
取直线PE与平面ABC所成角的最大值为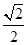 …………(4分)
…………(4分)
(2)如图所示,连接DE、CE,∵D、E、F分别是所在棱的中点,
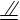
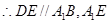
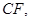

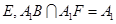 ,
,
又平面EDC//平面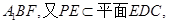
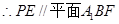 ………………………………………………………(8分)
………………………………………………………(8分)
(3)解法一 由(2)可知,直线PE与平面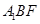 的距离等于两平行平面EDC与平面
的距离等于两平行平面EDC与平面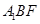 的距离,即点
的距离,即点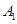 到平面EDC的距离,亦即A到平面EDC的距离.设A到平面EDC的距离为
到平面EDC的距离,亦即A到平面EDC的距离.设A到平面EDC的距离为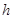 ,又
,又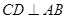 ,平面
,平面 且平面
且平面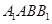 ,又
,又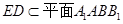 ,
,
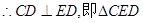 为直角三角形.
为直角三角形.
由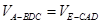 ,得
,得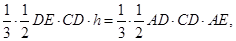
 ………………………………………… (12分)
………………………………………… (12分)
解法二 由(1)知,平面EDC//平面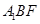 ,故平面
,故平面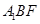 的法向量也为
的法向量也为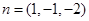 .又E到平面
.又E到平面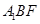 的距离,即为向量
的距离,即为向量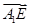 在法向量n上的投影的绝对值,
在法向量n上的投影的绝对值,
又 =
=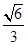

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目