Question

.（本小题满分12分）
如图甲，在平面四边形ABCD中，已知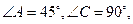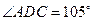,,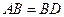现将四边形ABCD沿BD折起，使平面ABD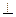平面BDC（如图乙），设点E、F分别为棱AC、AD的中点．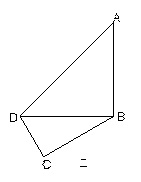

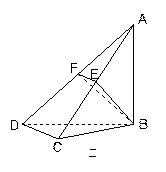
（1）求证：DC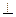平面ABC；
（2）设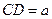，求三棱锥A－BFE的体积．

Answer 1

解：（1）证明：在图甲中∵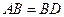且∴ ,
即----------------------------------------------2分
在图乙中，∵平面ABD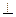平面BDC ， 且平面ABD平面BDC＝BD
∴AB⊥底面BDC，∴AB⊥CD．-----------------------------------4分
又，∴DC⊥BC,且
∴DC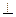平面ABC．---------------------------------------6分
（2）解法1：∵E、F分别为AC、AD的中点

∴EF//CD，又由（1）知，DC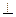平面ABC，
∴EF⊥平面ABC，--------------------------------------------7分
∴-------------------------8分
在图甲中，∵, ∴,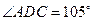
由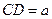得 ,--------------------------10分
∴   ∴
∴-------------------------------------------12分

解析