题目内容
设数列{an}的前n项和为Sn，令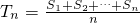
，称Tn为数列a1，a2，…，an的“理想数”，已知数列a1，a2，…，a500的“理想数”为2004，那么数列2，a1，a2，…，a500的“理想数”为________．
2002
分析：由公式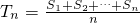得，数列a1，a2，…，a500的“理想数”为
，从而得s1+s2+…+s500；所以数列2，a1，a2，…，a500的“理想数”为：
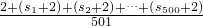，得出答案．
解答：根据题意得，数列a1，a2，…，a500的“理想数”为=2004，
即s1+s2+…+s500=2004×500；∴数列2，a1，a2，…，a500的“理想数”为：=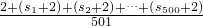
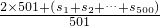=2+
=2+2000=2002；
故答案为：2002．
点评：本题考查了数列应用的一个新定义题目，解题时要弄清题意，捕捉解题信息，从而得出结论．
分析：由公式
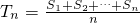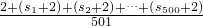得，数列a1，a2，…，a500的“理想数”为，从而得s1+s2+…+s500；所以数列2，a1，a2，…，a500的“理想数”为：，得出答案．解答：根据题意得，数列a1，a2，…，a500的“理想数”为
=2004，即s1+s2+…+s500=2004×500；∴数列2，a1，a2，…，a500的“理想数”为：
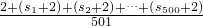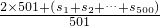==2+=2+2000=2002；故答案为：2002．
点评：本题考查了数列应用的一个新定义题目，解题时要弄清题意，捕捉解题信息，从而得出结论．
练习册系列答案
相关题目