题目内容
若函数 满足下列条件:在定义域内存在
满足下列条件:在定义域内存在 使得
使得 成立,则称函数
成立,则称函数 具有性质
具有性质 ;反之,若
;反之,若 不存在,则称函数
不存在,则称函数 不具有性质
不具有性质 .
.
(1)证明:函数 具有性质
具有性质 ,并求出对应的
,并求出对应的 的值;
的值;
(2)已知函数 具有性质
具有性质 ,求
,求 的取值范围;
的取值范围;
(3)试探究形如① 、②
、② 、③
、③ 、④
、④ 、⑤
、⑤ 的函数,指出哪些函数一定具有性质
的函数,指出哪些函数一定具有性质 ?并加以证明.
?并加以证明.
 满足下列条件:在定义域内存在
满足下列条件:在定义域内存在 使得
使得 成立,则称函数
成立,则称函数 具有性质
具有性质 ;反之,若
;反之,若 不存在,则称函数
不存在,则称函数 不具有性质
不具有性质 .
.(1)证明:函数
 具有性质
具有性质 ,并求出对应的
,并求出对应的 的值;
的值;(2)已知函数
 具有性质
具有性质 ,求
,求 的取值范围;
的取值范围;(3)试探究形如①
 、②
、② 、③
、③ 、④
、④ 、⑤
、⑤ 的函数,指出哪些函数一定具有性质
的函数,指出哪些函数一定具有性质 ?并加以证明.
?并加以证明.(1)证明: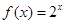 代入
代入 得:
得: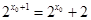
即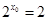 ,解得
,解得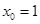
∴函数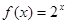 具有性质
具有性质 .
.
(2)解: 的定义域为R,且可得
的定义域为R,且可得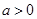 ,
,
∵ 具有性质
具有性质 ,
,
∴存在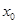 ,使得
,使得 ,代入得
,代入得
化为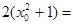
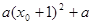
整理得: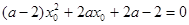 有实根
有实根
①若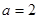 ,得
,得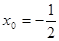 ,满足题意;
,满足题意;
②若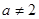 ,则要使
,则要使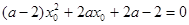 有实根,只需满足
有实根,只需满足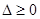 ,
,
即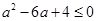 ,解得
,解得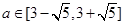
∴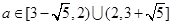
综合①②,可得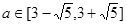
(3)解法一:函数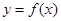 恒具有性质
恒具有性质 ,即关于
,即关于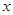 的方程
的方程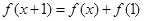 (*)恒有解.
(*)恒有解.
①若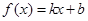 ,则方程(*)可化为
,则方程(*)可化为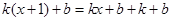
整理,得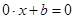
当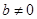 时,关于
时,关于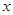 的方程(*)无解
的方程(*)无解
∴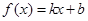 不恒具备性质
不恒具备性质 ;
;
②若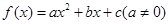 ,则方程(*)可化为
,则方程(*)可化为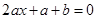 ,解得
,解得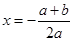 .
.
∴函数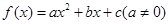 一定具备性质
一定具备性质 .
.
③若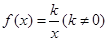 ,则方程(*)可化为
,则方程(*)可化为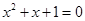 无解
无解
∴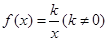 不具备性质
不具备性质 ;
;
④若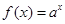 ,则方程(*)可化为
,则方程(*)可化为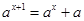 ,化简得
,化简得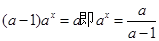
当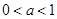 时,方程(*)无解
时,方程(*)无解
∴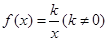 不恒具备性质
不恒具备性质 ;
;
⑤若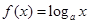 ,则方程(*)可化为
,则方程(*)可化为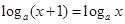 ,化简得
,化简得
显然方程无解
∴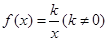 不具备性质
不具备性质 ;
;
综上所述,只有函数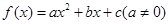 一定具备性质
一定具备性质 .
.
解法二:函数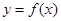 恒具有性质
恒具有性质 ,即函数
,即函数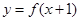 与
与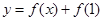 的图象恒有公共点.由图象分析,可知函数
的图象恒有公共点.由图象分析,可知函数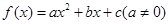 一定具备性质
一定具备性质 .
.
下面证明之:
方程 可化为
可化为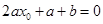 ,解得
,解得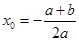 .
.
∴函数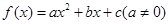 一定具备性质
一定具备性质 .
.
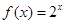 代入
代入 得:
得: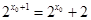
即
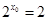 ,解得
,解得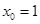
∴函数
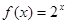 具有性质
具有性质 .
. (2)解:
 的定义域为R,且可得
的定义域为R,且可得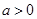 ,
,∵
 具有性质
具有性质 ,
,∴存在
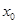 ,使得
,使得 ,代入得
,代入得
化为
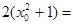
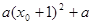
整理得:
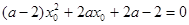 有实根
有实根①若
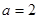 ,得
,得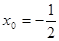 ,满足题意;
,满足题意; ②若
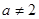 ,则要使
,则要使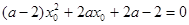 有实根,只需满足
有实根,只需满足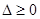 ,
,即
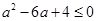 ,解得
,解得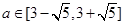
∴
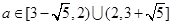
综合①②,可得
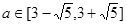
(3)解法一:函数
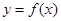 恒具有性质
恒具有性质 ,即关于
,即关于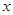 的方程
的方程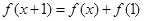 (*)恒有解.
(*)恒有解.①若
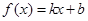 ,则方程(*)可化为
,则方程(*)可化为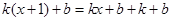
整理,得
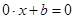
当
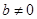 时,关于
时,关于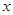 的方程(*)无解
的方程(*)无解∴
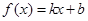 不恒具备性质
不恒具备性质 ;
;②若
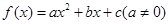 ,则方程(*)可化为
,则方程(*)可化为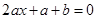 ,解得
,解得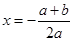 .
.∴函数
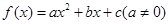 一定具备性质
一定具备性质 .
.③若
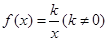 ,则方程(*)可化为
,则方程(*)可化为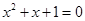 无解
无解∴
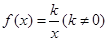 不具备性质
不具备性质 ;
;④若
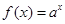 ,则方程(*)可化为
,则方程(*)可化为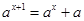 ,化简得
,化简得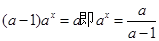
当
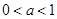 时,方程(*)无解
时,方程(*)无解∴
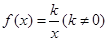 不恒具备性质
不恒具备性质 ;
;⑤若
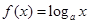 ,则方程(*)可化为
,则方程(*)可化为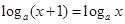 ,化简得
,化简得
显然方程无解
∴
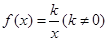 不具备性质
不具备性质 ;
;综上所述,只有函数
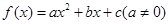 一定具备性质
一定具备性质 .
. 解法二:函数
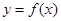 恒具有性质
恒具有性质 ,即函数
,即函数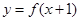 与
与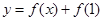 的图象恒有公共点.由图象分析,可知函数
的图象恒有公共点.由图象分析,可知函数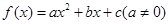 一定具备性质
一定具备性质 .
. 下面证明之:
方程
 可化为
可化为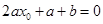 ,解得
,解得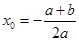 .
.∴函数
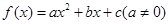 一定具备性质
一定具备性质 .
.略

练习册系列答案
相关题目
 且
且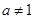 ,下列四组函数中表示相等函数的是( )
,下列四组函数中表示相等函数的是( )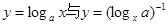


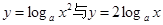

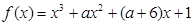 在
在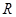 上没有极值,则实数
上没有极值,则实数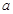 的取值范围
的取值范围 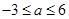
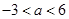
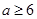 或
或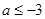
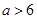 或
或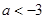
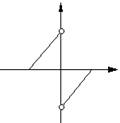
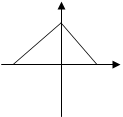
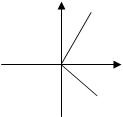
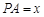 ,过点
,过点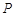 且与AB垂直的截面面积记为y,则
且与AB垂直的截面面积记为y,则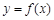 的图像是( )
的图像是( )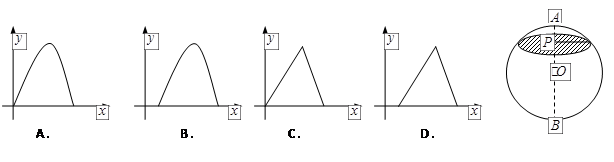
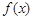 =
=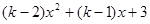 是偶函数,则
是偶函数,则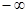 ,
,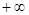 )内为减函数的是
)内为减函数的是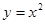
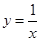
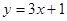
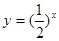
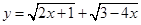 的定义域为( )
的定义域为( )