题目内容
设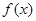 是定义在
是定义在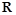 上的奇函数,且当
上的奇函数,且当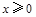 时,
时, ,若对任意
,若对任意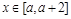 ,不等式
,不等式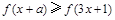 恒成立,则实数
恒成立,则实数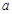 的取值范围是 .
的取值范围是 .
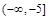
解析试题分析:因为,函数 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当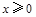 时,
时, ,
,
所以,当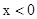 时,
时,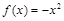
∴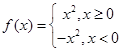 ,
,
∴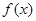 在R上是单调递增,且满足对任意
在R上是单调递增,且满足对任意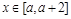 ,不等式
,不等式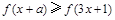 恒成立
恒成立
∴对任意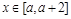 ,
,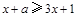 ,即
,即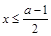 恒成立,
恒成立,
∴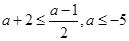 ,故答案为
,故答案为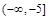 .
.
考点:函数的奇偶性,函数的单调性,简单不等式的解法.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
题目内容
设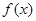 是定义在
是定义在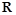 上的奇函数,且当
上的奇函数,且当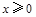 时,
时, ,若对任意
,若对任意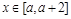 ,不等式
,不等式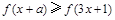 恒成立,则实数
恒成立,则实数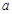 的取值范围是 .
的取值范围是 .
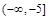
解析试题分析:因为,函数 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当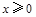 时,
时, ,
,
所以,当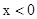 时,
时,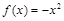
∴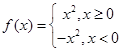 ,
,
∴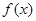 在R上是单调递增,且满足对任意
在R上是单调递增,且满足对任意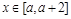 ,不等式
,不等式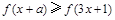 恒成立
恒成立
∴对任意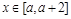 ,
,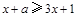 ,即
,即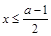 恒成立,
恒成立,
∴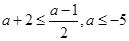 ,故答案为
,故答案为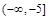 .
.
考点:函数的奇偶性,函数的单调性,简单不等式的解法.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案