题目内容
设函数f (x)＝cos(2x＋
)＋
sin2x＋2a
（1）求函数f (x)的单调递增区间
（2）当0≤x≤
时，f (x)的最小值为0，求a的值．
解：（Ⅰ）f (x)＝
cos2x＋
sin2x＋2a＝sin(2x＋
)＋2a．
由2kp－
≤2x＋≤2kp＋，得kp－
≤x≤kp＋（k∈Z）．
所以，f (x)的单调递增区间为[kp－,kp＋]（k∈Z）．
（Ⅱ）由0≤x≤
，得≤2x＋≤
，故≤sin(2x＋)≤1．
由f (x)的最小值为0，得＋2a＝0．解得a＝－
．
练习册系列答案
相关题目
元的一年定期储蓄。若年利率为
保持不变，且每年到期的存款本息均自动转为新的一年定期储蓄，到2014年1月1日，甲去银行不再存款，而是将所有存款的本息全部取回，则取回的金额是（ ）元.
的化简结果是 （ ）
B. 
C. 
D. 
作圆
的两条切线,切点分别为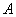
, 
,则直线
的方程为 （ ）
B．
C．
D．
=
的导函数是
D．y′=3
为虚数单位，复数
（ ）.
B 
C 
D 