题目内容
2.已知函数f(x)的定义域为R,若存在常数k>0,使|f(x)|≤$\frac{k}{2015}$|x|对一切实数x均成立,则称f(x)为“海宝”函数.给出下列函数:①f(x)=x2;②f(x)=sinx+cosx;③f(x)=$\frac{x}{{x}^{2}+x+1}$;④f(x)=3x+1
其中f(x)是“海宝”函数的序号为③.
分析 结合题中的新定义,取x=0时,可排除②④,对①中整理可得:2015|x|≤k,不存在常数k,
③中整理可得:$\frac{2015}{{x}^{2}+x+1}$≤k,只需求出$\frac{2015}{{x}^{2}+x+1}$的最大值即可.
解答 解:当x=0时,
②中f(0)=1,④中f(0)=2显然不成立,故不是“海宝”函数;
①中整理可得:2015|x|≤k,不存在常数k,使对一切实数x均成立,故不是“海宝”函数;
③中整理可得:$\frac{2015}{{x}^{2}+x+1}$≤k,对一切实数x均成立,
∵x2+x+1≥$\frac{3}{4}$,
∴$\frac{2015}{{x}^{2}+x+1}$≤$\frac{8060}{3}$,
∴k≥$\frac{8060}{3}$,故③正确.
故答案为 ③
点评 考查新定义,需对新定义理解透彻,利用新定义逐一判断.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
7.已知α=20°,则tanα+4sinα的值为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
11.已知a,b,c三个数成等差数列,其中a=5+2$\sqrt{6}$,c=5-2$\sqrt{6}$,则b的值为( )
| A. | 2$\sqrt{6}$ | B. | $\sqrt{6}$ | C. | 5 | D. | 10 |




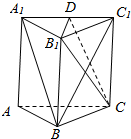 如图所示,棱柱ABC-A1B1C1的侧面BCC1B1是菱形,设D是A1C1上的点且A1B∥平面B1CD,则A1D:DC1的值为1.
如图所示,棱柱ABC-A1B1C1的侧面BCC1B1是菱形,设D是A1C1上的点且A1B∥平面B1CD,则A1D:DC1的值为1.