题目内容
已知椭圆C：
＋
＝1(a>b>0)的离心率为
，短轴一个端点到右焦点的距离为
.
(1)求椭圆C的方程。
(2)设直线l与椭圆C交于A、B两点，坐标原点O到直线l的距离为
，求△AOB面积的最大值．
解：(1)设椭圆的半焦距为c，依题意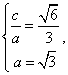
∴b＝1.∴所求椭圆方程为
＋y2＝1. .。。。。。。。。（4分）
(2)设A(x1，y1)，B(x2，y2)，
①当AB⊥x轴时，|AB|＝，
②当AB与x轴不垂直时，设直线AB的方程为y＝kx＋m.由已知
＝，得m2＝
(k2＋1)，把y＝kx＋m代入椭圆方程，整理得
(3k2＋1)x2＋6kmx＋3m2－3＝0∴x1＋x2＝
，x1x2＝
.
∴|AB|2＝(1＋k2)(x2－x1)2＝(1＋k2)
＝
＝
＝3＋
＝3＋
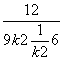(k≠0)
练习册系列答案
相关题目
＋
＝1（a＞b＞0）的离心率为
，过右焦点F且斜率为1的直线交椭圆C于A，B两点，N为弦AB的中点。
（
＝cos
＋sin
成立。
＋
＝1（a＞b＞0）的离心率为
，过右焦点F且斜率为1的直线交椭圆C于A，B两点，N为弦AB的
（
＝cos
＋sin
成立
＋
＝1（a＞b＞0）的离心率为
，过右焦点F且斜率为1的直线交椭圆C于A，B两点，N为弦AB的中点。
（
＝cos
＋sin
成立。w.w.w.k.s.5.u.c.o.m
＋
＝1（a＞b＞0）的离心率为
，过右焦点F且斜率为1的直线交椭圆C于A，B两点，N为弦AB的中点。
（
＝cos
＋sin
成立。
＋
＝1（a＞b＞0）的离心率为
，过右焦点F的直线l与C相交于A、B两点，当l的斜率为1时，坐标原点O到l的距离为
．
＝
＋
成立？若存在，求出所有的P的坐标与l的方程；若不存在，说明理由．