题目内容
 如图,在多面体ABDEC中,AE⊥平面ABC,BD∥AE,且AC=AB=BC=AE=1,BD=2,F为CD中点.
如图,在多面体ABDEC中,AE⊥平面ABC,BD∥AE,且AC=AB=BC=AE=1,BD=2,F为CD中点.(I)求证:EF∥平面ABC;
(II)求证:EF⊥平面BCD;
(III)求多面体ABDEC的体积.
分析:(Ⅰ)取BC中点G点,连接AG,FG,则四边形EFGA为平行四边形,于是EF∥AG,利用线面平行的判定定理即可证得EF∥平面ABC;
(Ⅱ)易证AG⊥平面BCD,而EF∥AG,从而由线面垂直的性质可得EF⊥平面BCD;
(Ⅲ)过C作CH⊥AB,则CH⊥平面ABDE易求CH=
,而VC-ABDE=
×S四边形ABDE×CH,计算即可.
(Ⅱ)易证AG⊥平面BCD,而EF∥AG,从而由线面垂直的性质可得EF⊥平面BCD;
(Ⅲ)过C作CH⊥AB,则CH⊥平面ABDE易求CH=
| ||
| 2 |
| 1 |
| 3 |
解答:证明: (Ⅰ)取BC中点G点,连接AG,FG,
(Ⅰ)取BC中点G点,连接AG,FG,
∵F,G分别为DC,BC中点,
∴FG
DB
EA,
∴四边形EFGA为平行四边形,
∴EF∥AG.
又∵EF?平面ABC,AG?平面ABC,
∴EF∥平面ABC,….4分
(2)∵AE⊥面ABC,BD∥AE,
∴DB⊥平面ABC,
又∵DB?平面BCD,
∴平面ABC⊥平面BCD,
又∵G为 BC中点且AC=AB=BC,
∴AG⊥BC,
∴AG⊥平面BCD,
又∵EF∥AG,
∴EF⊥平面BCD ….8分
(3)过C作CH⊥AB,则CH⊥平面ABDE且CH=
,
∴VC-ABDE=
×S四边形ABDE×CH
=
×
×1×
=
…12分.
 (Ⅰ)取BC中点G点,连接AG,FG,
(Ⅰ)取BC中点G点,连接AG,FG,∵F,G分别为DC,BC中点,
∴FG
| ||
. |
| 1 |
| 2 |
| ||
. |
∴四边形EFGA为平行四边形,
∴EF∥AG.
又∵EF?平面ABC,AG?平面ABC,
∴EF∥平面ABC,….4分
(2)∵AE⊥面ABC,BD∥AE,
∴DB⊥平面ABC,
又∵DB?平面BCD,
∴平面ABC⊥平面BCD,
又∵G为 BC中点且AC=AB=BC,
∴AG⊥BC,
∴AG⊥平面BCD,
又∵EF∥AG,
∴EF⊥平面BCD ….8分
(3)过C作CH⊥AB,则CH⊥平面ABDE且CH=
| ||
| 2 |
∴VC-ABDE=
| 1 |
| 3 |
=
| 1 |
| 3 |
| (1+2) |
| 2 |
| ||
| 2 |
=
| ||
| 4 |
点评:本题考查直线与平面平行的判定与直线与平面垂直的判定,掌握直线与平面平行与垂直的判定定理是解决问题之关键,考查分析与运算、准确书写与完整表达的能力,属于中档题.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
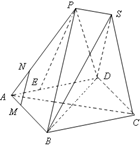 已知四边形ABCD为菱形,AB=6,∠BAD=60°,两个正三棱锥P-ABD、S-BCD(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,如图,E、M、N分别在AD、
已知四边形ABCD为菱形,AB=6,∠BAD=60°,两个正三棱锥P-ABD、S-BCD(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,如图,E、M、N分别在AD、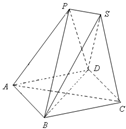 如图,已知放在同一平面上的两个正三棱锥P-ABD、S-BCD(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等.若AB=6,二面角P-BD-S的余弦值为
如图,已知放在同一平面上的两个正三棱锥P-ABD、S-BCD(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等.若AB=6,二面角P-BD-S的余弦值为
 .
.
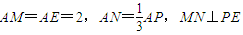 .
.