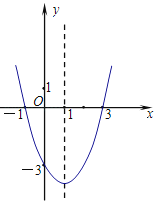题目内容
【题目】对于函数
、
、
，如果存在实数
使得
，那么称
为
、
的生成函数．
(1) 下面给出两组函数， 
是否分别为
、
的生成函数？并说明理由；
第一组： 
， 
， 
第二组： 
， 
， 
；
(2) 设
， 
， 
，生成函数
．若不等式
在
上有解，求实数
的取值范围；
(3) 设
， 
，取
，生成函数
图像的最低点坐标为
．若对于任意正实数
，且
，试问是否存在最大的常数
，使
恒成立？如果存在，求出这个
的值；如果不存在，请说明理由．
【答案】(1)见解析 (2) 
(3) 
为289
【解析】试题分析：（1）由条件利用生成函数的定义，判断生成函数
是否分别为是
、
的生成函数，从而得出结论；（2）
有解等价于
在
上有解，只需
小于函数
在
的最大值即可；（3）先求出函数
的最小值为289，只需
即可.
试题解析：(1)第一组： 
是
、
的生成函数，因为存在
使
第二组： 
不是
、
的生成函数，因为若存在
使得
，则有
故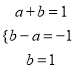
，而此方程无解，所以
不是
、
的生成函数 .
(2) 依题意，有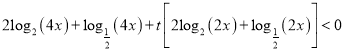
在
上有解
化简得： 
即
在
上有解
函数
在
的最大值为
故实数
的取值范围为
(3) 存在最大的常数
为289
依题意， 
，由
当且仅当
即
时等号成立得：
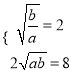，解得： 
，故
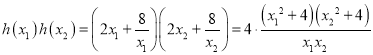
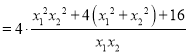
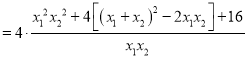
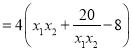
正数
，满足/span>
，故
当且仅当
时等号成立
函数
的最小值为289，故最大的常数
为289．
【方法点晴】本题主要考查对数的运算、二次函数的性质以及不等式恒成立问题，属于难题．不等式恒成立问题常见方法：① 分离参数
恒成立(
可)或
恒成立（
即可）；② 数形结合(
图象在
上方即可)；③ 讨论最值
或
恒成立；④ 讨论参数.本题是利用方法 ① 求得
的最大值.
练习册系列答案
阅读快车系列答案
相关题目
