题目内容
已知函数y=f(x)的图象与函数y=ax(a>0且a≠1)的图象关于直线y=x对称,记g(x)=f(x)[f(x)+f(2)-1].若y=g(x)在区间 上是增函数,则实数a的取值范围是( )
上是增函数,则实数a的取值范围是( )A.[2,+∞)
B.(0,1)∪(1,2)
C.

D.

【答案】分析:先表述出函数f(x)的解析式然后代入将函数g(x)表述出来,然后对底数a进行讨论即可得到答案.
解答:解:已知函数y=f(x)的图象与函数y=ax(a>0且a≠1)的图象关于直线y=x对称,
则f(x)=logax,记g(x)=f(x)[f(x)+f(2)-1]=(logax)2+(loga2-1)logax.
当a>1时,
若y=g(x)在区间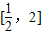 上是增函数,y=logax为增函数,
上是增函数,y=logax为增函数,
令t=logax,t∈[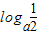 ,loga2],要求对称轴
,loga2],要求对称轴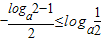 ,矛盾;
,矛盾;
当0<a<1时,若y=g(x)在区间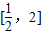 上是增函数,y=logax为减函数,
上是增函数,y=logax为减函数,
令t=logax,t∈[loga2,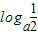 ],要求对称轴
],要求对称轴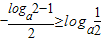 ,
,
解得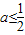 ,
,
所以实数a的取值范围是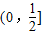 ,
,
故选D.
点评:本题主要考查指数函数与对数函数互为反函数.这里注意指数函数和对数函数的增减性与底数的大小有关,即当底数大于1时单调递增,当底数大于0小于1时单调递减.
解答:解:已知函数y=f(x)的图象与函数y=ax(a>0且a≠1)的图象关于直线y=x对称,
则f(x)=logax,记g(x)=f(x)[f(x)+f(2)-1]=(logax)2+(loga2-1)logax.
当a>1时,
若y=g(x)在区间
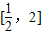 上是增函数,y=logax为增函数,
上是增函数,y=logax为增函数,令t=logax,t∈[
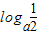 ,loga2],要求对称轴
,loga2],要求对称轴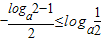 ,矛盾;
,矛盾;当0<a<1时,若y=g(x)在区间
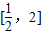 上是增函数,y=logax为减函数,
上是增函数,y=logax为减函数,令t=logax,t∈[loga2,
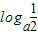 ],要求对称轴
],要求对称轴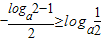 ,
,解得
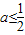 ,
,所以实数a的取值范围是
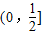 ,
,故选D.
点评:本题主要考查指数函数与对数函数互为反函数.这里注意指数函数和对数函数的增减性与底数的大小有关,即当底数大于1时单调递增,当底数大于0小于1时单调递减.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为 已知函数y=f(x)的图象如图,则满足
已知函数y=f(x)的图象如图,则满足