题目内容
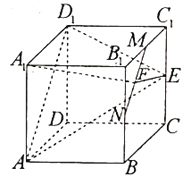
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() ,
,![]() ,
,![]() 的中点.
的中点.

(I)证明:直线![]() 与
与![]() 共面;
共面;
(Ⅱ)证明:平面![]() 平面
平面![]() ;并试写出
;并试写出![]() 到平面
到平面![]() 的距离(不必写出计算过程).
的距离(不必写出计算过程).
【答案】(I)证明见解析;(Ⅱ)证明见解析.
【解析】
(I)由中位线的性质可得![]() ,再由棱柱的性质可得
,再由棱柱的性质可得![]() ,根据平行线的传递性可得
,根据平行线的传递性可得![]() ,从而得到四点共面,即可得证;
,从而得到四点共面,即可得证;
(Ⅱ)首先可得![]() ,再由线面垂直的性质得到
,再由线面垂直的性质得到![]() ,从而得到
,从而得到![]() 平面
平面![]() ,再根据
,再根据![]() ,即可得到
,即可得到![]() 平面
平面![]() ,从而得证;设
,从而得证;设![]() ,则
,则![]() 平面
平面![]() 平面
平面![]() ,过
,过![]() 作
作![]() 于
于![]() ,可得
,可得![]() 即为
即为![]() 到平面
到平面![]() 的距离,再在三角形中利用勾股定理及相似三角形的性质计算可得.
的距离,再在三角形中利用勾股定理及相似三角形的性质计算可得.
解:(I)证明:![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() ,
,
由棱柱性质易得![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() 四点共面,即直线
四点共面,即直线![]() 与
与![]() 共面.
共面.
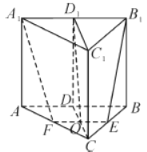
(Ⅱ)同(I)易证四边形![]() 为平行四边形,又
为平行四边形,又![]() ,
,![]() 为
为![]() 中点,则
中点,则![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]() ,又
,又![]() ,
,![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() 得证.
得证.
![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
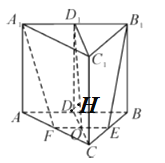
(解答)如图,设![]() ,则
,则![]() 平面
平面![]() 平面
平面![]() ,过
,过![]() 作
作![]() 于
于![]() ,可得
,可得![]() 即为
即为![]() 到平面
到平面![]() 的距离.在
的距离.在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,又
,又![]() ,则在
,则在![]() 中,
中,![]()
故![]() ,即
,即![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案【题目】响应“文化强国建设”号召,某市把社区图书阅览室建设增列为重要的民生工程.为了解市民阅读需求,随机抽取市民200人做调查,统计显示,男士喜欢阅读古典文学的有64人,不喜欢的有56人;女士喜欢阅读古典文学的有36人,不喜欢的有44人.
(1)能否在犯错误的概率不超过0.25的前提下认为喜欢阅读古典文学与性别有关系?
(2)为引导市民积极参与阅读,有关部门牵头举办市读书交流会,从这200人中筛选出5名男代表和4名代表,其中有3名男代表和2名女代表喜欢古典文学.现从这9名代表中任选3名男代表和2名女代表参加交流会,记![]() 为参加交流会的5人中喜欢古典文学的人数,求
为参加交流会的5人中喜欢古典文学的人数,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
附:![]() ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |
【题目】目前有声书正受着越来越多人的喜爱.某有声书公司为了解用户使用情况,随机选取了![]() 名用户,统计出年龄分布和用户付费金额(金额为整数)情况如下图.
名用户,统计出年龄分布和用户付费金额(金额为整数)情况如下图.
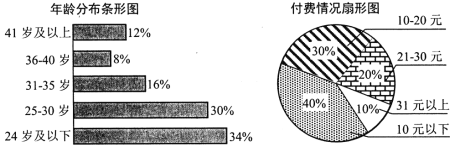
有声书公司将付费高于![]() 元的用户定义为“爱付费用户”,将年龄在
元的用户定义为“爱付费用户”,将年龄在![]() 岁及以下的用户定义为“年轻用户”.已知抽取的样本中有
岁及以下的用户定义为“年轻用户”.已知抽取的样本中有![]() 的“年轻用户”是“爱付费用户”.
的“年轻用户”是“爱付费用户”.
(1)完成下面的![]() 列联表,并据此资料,能否有
列联表,并据此资料,能否有![]() 的把握认为用户“爱付费”与其为“年轻用户”有关?
的把握认为用户“爱付费”与其为“年轻用户”有关?
爱付费用户 | 不爱付费用户 | 合计 | |
年轻用户 | |||
非年轻用户 | |||
合计 |
(2)若公司采用分层抽样方法从“爱付费用户”中随机选取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人进行访谈,求抽取的
人进行访谈,求抽取的![]() 人恰好都是“年轻用户”的概率.
人恰好都是“年轻用户”的概率.
|
|
|
|
|
|
|
|
|
|
|
|
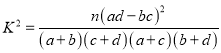 .
.