题目内容
(本小题满分12分)
椭圆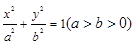 的左、右焦点分别为
的左、右焦点分别为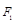 、
、 ,点
,点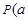 ,
,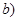 满足
满足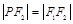 .
.
(1)求椭圆的离心率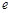 ;
;
(2)设直线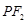 与椭圆相交于
与椭圆相交于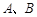 两点,若直线
两点,若直线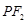 与圆
与圆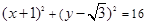 相交于
相交于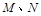 两点,且
两点,且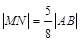 ,求椭圆的方程.
,求椭圆的方程.
椭圆
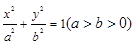 的左、右焦点分别为
的左、右焦点分别为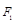 、
、 ,点
,点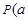 ,
,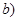 满足
满足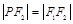 .
.(1)求椭圆的离心率
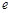 ;
;(2)设直线
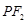 与椭圆相交于
与椭圆相交于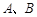 两点,若直线
两点,若直线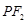 与圆
与圆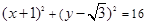 相交于
相交于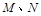 两点,且
两点,且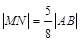 ,求椭圆的方程.
,求椭圆的方程.(1) (2)
(2)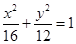
 (2)
(2)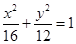
试题分析:解:(1)设
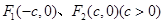 ,因为
,因为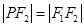 ,
,所以
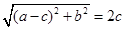 . …………………………………………………………………2分
. …………………………………………………………………2分整理得
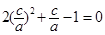 ,得
,得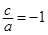 (舍),或
(舍),或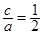 .
.所以
 .……………………………………………………………………………………4分
.……………………………………………………………………………………4分(2)由(1)知
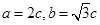 ,椭圆方程
,椭圆方程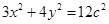 ,
,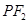 的方程为
的方程为 .
.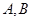 两点的坐标满足方程组
两点的坐标满足方程组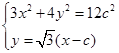 ,消去
,消去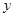 并整理,得
并整理,得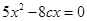 .
.解得
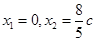 .得方程组的解
.得方程组的解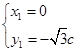 ,
,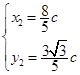 .………………………7分
.………………………7分不妨设
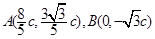 ,则
,则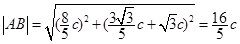 .
.于是
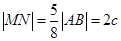 .
.圆心
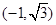 到直线
到直线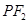 的距离
的距离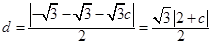 .………………10分
.………………10分因为
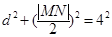 ,所以
,所以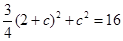 ,整理得
,整理得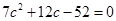 .
.得
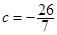 (舍),或
(舍),或 .
.所以椭圆方程为
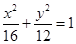 . ……………………………………………………………12分
. ……………………………………………………………12分点评:解决该试题的关键是能利用其性质得到关系式,同时联立方程组,求解交点的坐标,进而得到弦长,以及点到直线距离得到结论,属于基础题。

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
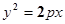 与直线
与直线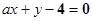 交于A,B两点,其中A点的坐标是
交于A,B两点,其中A点的坐标是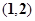 .该抛物线的焦点为F,则
.该抛物线的焦点为F,则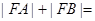 ( )
( )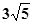
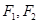 是椭圆
是椭圆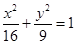 的两个焦点,经过点
的两个焦点,经过点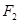 的直线交椭圆于点
的直线交椭圆于点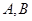 ,若
,若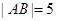 ,则
,则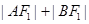 等于( )
等于( )
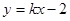 相交于不同的两点A、B,且AB中点横坐标为2,求k的值.
相交于不同的两点A、B,且AB中点横坐标为2,求k的值.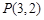 且与双曲线
且与双曲线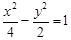 有相同渐近线方程的双曲线的标准方程为 .
有相同渐近线方程的双曲线的标准方程为 .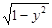 恰有一个公共点,则k的取值范围是___________
恰有一个公共点,则k的取值范围是___________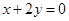 与圆
与圆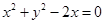 的交点为A、B,
的交点为A、B,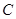 的两焦点是
的两焦点是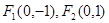 ,离心率
,离心率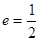 .
.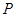 在椭圆
在椭圆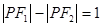 ,求DPF1F2的面积.
,求DPF1F2的面积.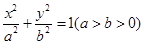 的两个焦点为
的两个焦点为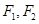 ,椭圆的离心率为
,椭圆的离心率为 ,
, 点是椭圆上任意一点, 且
点是椭圆上任意一点, 且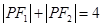 ,
,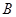 为直角顶点作椭圆的内接等腰直角三角形
为直角顶点作椭圆的内接等腰直角三角形 ,这样的等腰直角三角形是否存在?若存在请说明有几个、并求出直角边所在直线方程?若不存在,请说明理由.
,这样的等腰直角三角形是否存在?若存在请说明有几个、并求出直角边所在直线方程?若不存在,请说明理由.