题目内容
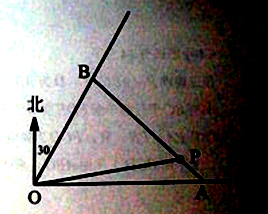
【题目】如图,某商业中心O有通往正东方向和北偏东30方向的两条街道,某公园P位于商业中心北偏东![]() 角(
角(![]() ),且与商业中心O的距离为
),且与商业中心O的距离为![]() 公里处,现要经过公园P修一条直路分别与两条街道交汇于A,B两处。
公里处,现要经过公园P修一条直路分别与两条街道交汇于A,B两处。
(1)当AB沿正北方向时,试求商业中心到A,B两处的距离和;
(2)若要使商业中心O到A,B两处的距离和最短,请确定A,B的最佳位置。
【答案】(1)13.5km.(2)商业中心到A、B两处的距离和最短为9km,此时OA=6km,OB=3km
【解析】
试题分析:(1)建立直角坐标系表示图中各量关系是解题关键:![]() ,OB=2OA=9,商业中心到A、B两处的距离和为13.5km.(2)当AB与
,OB=2OA=9,商业中心到A、B两处的距离和为13.5km.(2)当AB与![]() 轴不垂直时,设AB:
轴不垂直时,设AB:![]() ,则
,则![]() ,又直线OB的方程为
,又直线OB的方程为![]() ,所以
,所以![]() ,
,![]() ,从而
,从而![]() ,其中
,其中![]() ,或
,或![]() .利用导数可得当
.利用导数可得当![]() 时,
时,![]() 有极小值也是最小值为9km;此时OA=6km,OB=3km,
有极小值也是最小值为9km;此时OA=6km,OB=3km,
试题解析:
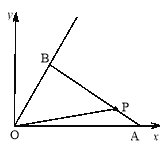
(1)以O为原点,OA所在直线为![]() 轴建立坐标系.设
轴建立坐标系.设![]() ,
,
∵![]() ,
,![]() ∴
∴![]() ,
,![]() ,
,
则![]() ,
,![]() , 4分
, 4分
依题意,AB⊥OA,则OA=![]() ,OB=2OA=9,商业中心到A、B两处的距离和为13.5km. 7分
,OB=2OA=9,商业中心到A、B两处的距离和为13.5km. 7分
(2)
方法1:当AB与![]() 轴不垂直时,设AB:
轴不垂直时,设AB:![]() ,①
,①
令![]() ,得
,得![]() ;由题意,直线OB的方程为
;由题意,直线OB的方程为![]() ,②
,②
解①②联立的方程组,得![]() ,∴
,∴![]() ,
,
∴![]() ,由
,由![]() ,
,![]() ,得
,得![]() ,或
,或![]() . 11分
. 11分
![]() ,令
,令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 是减函数;当
是减函数;当![]() 时,
时,![]() ,
,![]() 是增函数,
是增函数,
∴当![]() 时,
时,![]() 有极小值为9km;当
有极小值为9km;当![]() 时,
时,![]() ,
,![]() 是减函数,结合(1)知
是减函数,结合(1)知![]() km.
km.
综上所述,商业中心到A、B两处的距离和最短为9km,此时OA=6km,OB=3km,
方法2:如图,过P作PM//OA交OB于M,PN//OB交OA于N,设∠BAO=![]() ,
,
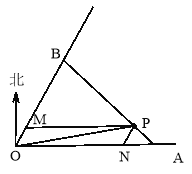
△OPN中![]() ,得PN=1,ON=4=PM,
,得PN=1,ON=4=PM,
△PNA中∠NPA=120°-![]() ∴
∴![]() 得
得![]()
同理在△PMB中,![]() ,得
,得![]() ,
,
![]() , 13分
, 13分
当且仅当![]() 即
即![]() 即
即![]() 时取等号.
时取等号.
方法3:若设点![]() ,则AB:
,则AB: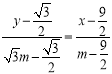 ,得
,得![]() ,
,
∴![]() , 13分
, 13分
当且仅当![]() 即
即![]() 时取等号.
时取等号.
方法4:设![]() ,AB:
,AB: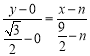 ,得
,得![]() ,
,
![]() , 13分
, 13分
当且仅当![]() 即
即![]() 时取等号.
时取等号.
答:A选地址离商业中心6km,B离商业中心3km为最佳位置. 15分

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
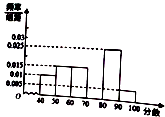
冲刺100分单元优化练考卷系列答案【题目】某市政府为了实施政府绩效管理、创新政府公共服务模式、提高公共服务效率.实施了“政府承诺,等你打分”民意调查活动,通过问卷调查了学生、在职人员、退休人员共250人,统计结果表不幸被污损,如表:
学生 | 在职人员 | 退休人员 | |
满意 |
|
| 78 |
不满意 | 5 |
| 12 |
若在所调查人员中随机抽取1人,恰好抽到学生的概率为0.32.
(1)求满意学生的人数;
(2)现用分层抽样的方法在所调查的人员中抽取25人,则在职人员应抽取多少人?
(3)若满意的在职人员为77,则从问卷调查中填写不满意的“学生和在职人员”中选出2人进行访谈,求这2人中包含了两类人员的概率.