题目内容
设集合M=
．
（1） 若a=1求M；
（2） 若1∈M，求a的取值范围；
（3） 若2∉M，求a的取值范围．．
解：（1）因为a=1代入集合，所以：
解得M=（-∞，-1）∪（2，+∞）．
（2）因为1∈M代入不等式，所以：
解得：
．
（3）若2∈M，即
则：a的取值范围为：
．
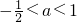所以满足2∉M的
所以答案为：．
分析：对于（1） 若a=1求M；把a=1代入集合中的不等式，解出不等式即可得到答案．
对于（2） 若1∈M，求a的取值范围；因为1∈M，吧x=1代入不等式，求不等式成立时的a范围即可．
对于（3） 若2∉M，求a的取值范围．可以同（2）的方法求其反面2∈M时a范围，再求得它的补集即可．
点评：此题主要考查元素与集合关系的判断问题，其中涉及到不等式的求解问题，对于此类问题较简单在高考中多在填空选择题的形式出现，计算量小属于基础题目．
解得M=（-∞，-1）∪（2，+∞）．
（2）因为1∈M代入不等式，所以：
解得：
．（3）若2∈M，即
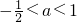则：a的取值范围为：．所以满足2∉M的
所以答案为：
．分析：对于（1） 若a=1求M；把a=1代入集合中的不等式，解出不等式即可得到答案．
对于（2） 若1∈M，求a的取值范围；因为1∈M，吧x=1代入不等式，求不等式成立时的a范围即可．
对于（3） 若2∉M，求a的取值范围．可以同（2）的方法求其反面2∈M时a范围，再求得它的补集即可．
点评：此题主要考查元素与集合关系的判断问题，其中涉及到不等式的求解问题，对于此类问题较简单在高考中多在填空选择题的形式出现，计算量小属于基础题目．
练习册系列答案
相关题目
设集合M={0，1，2，3，4}，N={x∈Z||x|＜2}，则M∩N为（ ）
| A、（-1，2） | B、（0，1） | C、{-1，0，1} | D、{0，1} |