题目内容

若直角△ABC的内切圆与斜边AB相切于点D，且AD=1，BD=2，则△ABC的面积为
2
2
．
分析：设内切圆半径为r，由勾股定理可得（1+r）2+（2+r）2=9，可得r2+3r=2，再根据△ABC的面积为 
1
2
×（1+r）（2+r），运算求得结果．
解答：解：由于直角△ABC的内切圆与斜边AB相切于点D，且AD=1，BD=2，设内切圆半径为r，
则由勾股定理可得（1+r）2+（2+r）2=9，∴r2+3r=2．
△ABC的面积为
1
2
×（1+r）（2+r）=
1
2
（r2+3r+2）=2，
故答案为 2．
点评：本题考查圆的切线性质，以及三角形中的几何计算，考查转化思想以及计算能力．
练习册系列答案
相关题目
如图，直角三角形ABC的顶点坐标A（-2，0），直角顶点B(0，-2
2
)，顶点C在x轴上，点P为线段OA的中点．
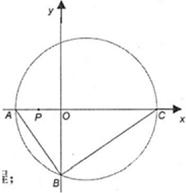精英家教网（1）求BC边所在直线方程；
（2）M为直角三角形ABC外接圆的圆心，求圆M的方程；
（3）若动圆N过点P且与圆M内切，求动圆N的圆心N的轨迹方程．

如图，直角三角形ABC的顶点坐标A(－2，0)，直角顶点B（0，－2），顶点C在x轴上，点P为线段OA的中点．

（Ⅰ）求BC边所在直线方程；

（Ⅱ）M为直角三角形ABC外接圆的圆心，求圆M的方程；

（Ⅲ）若动圆N过点P且与圆M内切，求动圆N的圆心N的轨迹方程．

 
如图，直角三角形ABC的顶点坐标A（-2，0），直角顶点，顶点C在x轴上，点P为线段OA的中点．
（1）求BC边所在直线方程；
（2）M为直角三角形ABC外接圆的圆心，求圆M的方程；
（3）若动圆N过点P且与圆M内切，求动圆N的圆心N的轨迹方程．
如图，直角三角形ABC的顶点坐标A（-2，0），直角顶点，顶点C在x轴上，点P为线段OA的中点．
（1）求BC边所在直线方程；
（2）M为直角三角形ABC外接圆的圆心，求圆M的方程；
（3）若动圆N过点P且与圆M内切，求动圆N的圆心N的轨迹方程．
如图，直角三角形ABC的顶点坐标A（-2，0），直角顶点，顶点C在x轴上，点P为线段OA的中点．
（1）求BC边所在直线方程；
（2）M为直角三角形ABC外接圆的圆心，求圆M的方程；
（3）若动圆N过点P且与圆M内切，求动圆N的圆心N的轨迹方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网