题目内容
已知f(x)=kx3-x2+x-5在R上单调递增,记△ABC的三内角A,B,C的对应边分别为a,b,c,若a2+c2≥b2+ac时,不等式f[m+sin2B+cos(A+C)]<f(2| m |
| 33 |
| 4 |
(1)求实数k的取值范围;
(2)求角cosB的取值范围;
(3)求实数m的取值范围.
分析:(1)对函数f(x)进行求导,利用函数的单调性判断出f′(x)>0恒成立进而判断出导函数的开口向上判断出k>0,判别式小于0求得k的范围.
(2)利用余弦定理和题设的不等式求得cosB的范围,进而求得B的范围.
(3)利用函数的单调性和题设的不等式建立不等式求得m的范围.
(2)利用余弦定理和题设的不等式求得cosB的范围,进而求得B的范围.
(3)利用函数的单调性和题设的不等式建立不等式求得m的范围.
解答:解:(1)由f(x)=kx3-x2+x-5知f′(x)=3kx2-2x+1,
∵f(x)在R上单调递增,∴f′(x)>0恒成立,
∴3k>0且△<0,即k>0且4-12k<0,∴k>
,
当△=0,即k=
时,f′(x)=3kx2-2x+1=(x-1)2,
∴x<1时f′(x)>0,x>1时,f′(x)>0,
即当k=
时,能使f(x)在R上单调递增,∴k≥
.
(2)∵a2+c2≥b2+ac,由余弦定理:cosB=
≥
=
,∴0<B≤
,
(3)∵f(x)在R上单调递增,且f[m+sin2B+cos(A+C)]<f(2
+
),
所以m+sin2B+cos(A+C)<2
+
-sin2B-cos(A+C)+
=-sin2B+cosB+
=cos2B+cosB+
=(cosB+
)2+7≥8,
故m-2
<8,即(
-1)2<9,-3<
-1<3,即0≤
<4,即0≤m<16.
∵f(x)在R上单调递增,∴f′(x)>0恒成立,
∴3k>0且△<0,即k>0且4-12k<0,∴k>
| 1 |
| 3 |
当△=0,即k=
| 1 |
| 3 |
∴x<1时f′(x)>0,x>1时,f′(x)>0,
即当k=
| 1 |
| 3 |
| 1 |
| 3 |
(2)∵a2+c2≥b2+ac,由余弦定理:cosB=
| a2+c2-b2 |
| 2ac |
| ac |
| 2ac |
| 1 |
| 2 |
| π |
| 3 |
(3)∵f(x)在R上单调递增,且f[m+sin2B+cos(A+C)]<f(2
| m |
| 33 |
| 4 |
所以m+sin2B+cos(A+C)<2
| m |
| 33 |
| 4 |
| 33 |
| 4 |
=-sin2B+cosB+
| 33 |
| 4 |
| 29 |
| 4 |
| 1 |
| 2 |
故m-2
| m |
| m |
| m |
| m |
点评:本题主要考查了余弦定理的应用,利用导函数研究函数的单调性以及函数.考查了基础知识的综合理解和应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
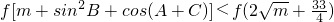 恒成立.
恒成立. 恒成立.
恒成立.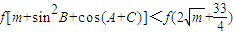 恒成立.
恒成立.