题目内容
【题目】已知椭圆![]() 左右焦点为
左右焦点为![]() ,左顶点为A(-2.0),上顶点为B,且∠
,左顶点为A(-2.0),上顶点为B,且∠![]() =
=![]() .
.
(1)求椭圆C的方程;
(2)探究![]() 轴上是否存在一定点P,过点P的任意直线与椭圆交于M、N不同的两点,M、N不与点A重合,使得
轴上是否存在一定点P,过点P的任意直线与椭圆交于M、N不同的两点,M、N不与点A重合,使得 ![]() 为定值,若存在,求出点P;若不存在,说明理由.
为定值,若存在,求出点P;若不存在,说明理由.
【答案】(1)![]() ;(2)存在点
;(2)存在点![]() 使得
使得![]() 为定值
为定值
【解析】
(1)由题意知a,结合∠![]() =
=![]() 可得c,.再利用a2=b2+c2,得b2即可.
可得c,.再利用a2=b2+c2,得b2即可.
(2)直线方程与椭圆方程联立可得根与系数的关系,利用数量积![]() 为定值,得到k与m的关系,即可得出结论.
为定值,得到k与m的关系,即可得出结论.
(1)由题意知:![]() 又∠
又∠![]() =
=![]() ,所以
,所以![]() 为正三角形,
为正三角形,
![]() ,
,![]() ,
,
椭圆C的方程为![]() ;
;
(2)设直线MN的为![]() ,M
,M![]() ,N
,N![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
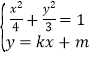 ,消去y得,
,消去y得,
![]() ,
,
由韦达定理![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
得![]() ,
,
![]() 为定值,则
为定值,则![]() ,即
,即![]() ,
,
得![]()
即存在点![]() 使得
使得![]() 为定值.
为定值.

练习册系列答案
相关题目
【题目】某书店销售刚刚上市的某高二数学单元测试卷,按事先拟定的价格进行5天试销,每种单价试销1天,得到如下数据:
单价x/元 | 18 | 19 | 20 | 21 | 22 |
销量y/册 | 61 | 56 | 50 | 48 | 45 |
(1)求试销![]() 天的销量的方差和
天的销量的方差和![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
附: 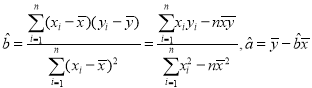 .
.
(2)预计以后的销售中,销量与单价服从上题中的回归直线方程,已知每册单元测试卷的成本是10元,为了获得最大利润,该单元测试卷的单价应定为多少元?