题目内容
若lnx≥
在x∈[1,+∞)上恒成立,则a的取值范围是
| (a-1)x2+a-3 |
| x2+1 |
(-∞,
]
| 5 |
| 2 |
(-∞,
]
.| 5 |
| 2 |
分析:把lnx≥
等价转化为lnx≥a-1-
,得到lnx+
≥a-1,从而原题等价转化为y=x+
在x∈[1,+∞)上的最小值不小于a-1,由此利用导数知识能够求出a的取值范围.
| (a-1)x2+a-3 |
| x2+1 |
| 1 |
| x2+1 |
| 1 |
| x2+1 |
| 1 |
| x2+1 |
解答:解:∵lnx≥
=a-1-
,
∴lnx+
≥a-1,
∵lnx≥
在x∈[1,+∞)上恒成立,
∴y=x+
在x∈[1,+∞)上的最小值不小于a-1,
∵y′=
-
,
令y′=
-
=0,得x=1,或x=-1(舍),
∴x∈[1,+∞)时,y′=
-
>0,
∴y=x+
在x∈[1,+∞)上是增函数,
∴当x=1时,y=x+
在x∈[1,+∞)上取最小值1+
=
,
故
≥a-1,
所以a≤
.
故答案为:(-∞,
].
| (a-1)x2+a-3 |
| x2+1 |
| 1 |
| x2+1 |
∴lnx+
| 1 |
| x2+1 |
∵lnx≥
| (a-1)x2+a-3 |
| x2+1 |
∴y=x+
| 1 |
| x2+1 |
∵y′=
| 1 |
| x |
| 4x |
| (x2+1)2 |
令y′=
| 1 |
| x |
| 4x |
| (x2+1)2 |
∴x∈[1,+∞)时,y′=
| 1 |
| x |
| 4x |
| (x2+1)2 |
∴y=x+
| 1 |
| x2+1 |
∴当x=1时,y=x+
| 1 |
| x2+1 |
| 1 |
| 12+1 |
| 3 |
| 2 |
故
| 3 |
| 2 |
所以a≤
| 5 |
| 2 |
故答案为:(-∞,
| 5 |
| 2 |
点评:本题考查实数的取值范围的求法,具体涉及到分离变量法、导数性质、等价转化思想等知识点的灵活运用,解题时要关键是lnx≥
在x∈[1,+∞)上恒成立等价转化为y=x+
在x∈[1,+∞)上的最小值不小于a-1.
| (a-1)x2+a-3 |
| x2+1 |
| 1 |
| x2+1 |

练习册系列答案
相关题目
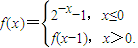 ,y=g(x)为k(x)=lnx+a+1在x=1处的切线方程,若方程f(x)-g(x)=0有且只有两个不相等的实数根,则实数a的取值范围是( )
,y=g(x)为k(x)=lnx+a+1在x=1处的切线方程,若方程f(x)-g(x)=0有且只有两个不相等的实数根,则实数a的取值范围是( )