题目内容
已知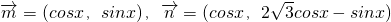 ,?>0,函数
,?>0,函数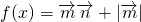 ,x1,x2是集合M={x|f(x)=1}中任意两个元素,且|x1-x2|的最小值为
,x1,x2是集合M={x|f(x)=1}中任意两个元素,且|x1-x2|的最小值为 .
.
(1)求?的值.
(2)在△ABC中,a,b,c分别是A,B,C的对边.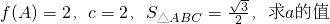 .
.
解:(1)由题意可知: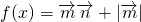
=cos2?x+2 sin?xcos?x-sin2?x+1
sin?xcos?x-sin2?x+1
=cos2?x sin2?x+1
sin2?x+1
=2sin(2?x+ )+1,
)+1,
又x1,x2是集合M={x|f(x)=1}中任意两个元素,且|x1-x2|的最小值为 ,
,
所以函数f(x)的半周期为 ,即
,即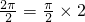 ,解得?=1
,解得?=1
(2)由(1)可知f(x)=2sin(2x+ )+1,进而可得2sin(2C+
)+1,进而可得2sin(2C+ )+1=2,
)+1=2,
化简得sin(2C+ )=
)= ,解得C=
,解得C= ,
,
由余弦定理可得 =(a+b)2-3ab,
=(a+b)2-3ab,
由S△ABC= absinC=
absinC= ab=
ab= ,可得ab=2,
,可得ab=2,
综合上面两式可得a+b= ,ab=2,故ab为方程
,ab=2,故ab为方程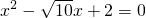 的根,
的根,
解得a=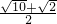 ,或
,或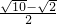
分析:(1)由向量的知识可对式子化简,由题意易得周期,进而可得?的值;
(2)代入解析式可得C,由余弦定理和面积公式联合可得关于ab的方程组,解之即可.
点评:本题考查向量的数量积,以及解三角形的知识,属中档题.
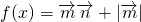
=cos2?x+2
 sin?xcos?x-sin2?x+1
sin?xcos?x-sin2?x+1=cos2?x
 sin2?x+1
sin2?x+1=2sin(2?x+
 )+1,
)+1,又x1,x2是集合M={x|f(x)=1}中任意两个元素,且|x1-x2|的最小值为
 ,
,所以函数f(x)的半周期为
 ,即
,即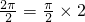 ,解得?=1
,解得?=1(2)由(1)可知f(x)=2sin(2x+
 )+1,进而可得2sin(2C+
)+1,进而可得2sin(2C+ )+1=2,
)+1=2,化简得sin(2C+
 )=
)= ,解得C=
,解得C= ,
,由余弦定理可得
 =(a+b)2-3ab,
=(a+b)2-3ab,由S△ABC=
 absinC=
absinC= ab=
ab= ,可得ab=2,
,可得ab=2,综合上面两式可得a+b=
 ,ab=2,故ab为方程
,ab=2,故ab为方程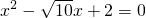 的根,
的根,解得a=
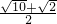 ,或
,或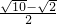
分析:(1)由向量的知识可对式子化简,由题意易得周期,进而可得?的值;
(2)代入解析式可得C,由余弦定理和面积公式联合可得关于ab的方程组,解之即可.
点评:本题考查向量的数量积,以及解三角形的知识,属中档题.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目