题目内容
数列{an}的首项为1,前n项和是Sn,存在常数A,B使an+Sn=An+B对任意正整数n都成立.(1)设A=0,求证:数列{an}是等比数列;
(2)设数列{an}是等差数列,若p<q,且
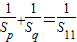 ,求p,q的值.
,求p,q的值.(3)设A>0,A≠1,且
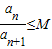 对任意正整数n都成立,求M的取值范围.
对任意正整数n都成立,求M的取值范围.
【答案】分析:(Ⅰ)A=0时,an+Sn=B,得出当n≥2时,由条件得,an-an-1+(Sn-Sn-1)=0即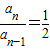 ,从而有数列{an}是等比数列;
,从而有数列{an}是等比数列;
(Ⅱ)设数列的公差为d,分别令n=1,2,3得关于A,B,C的方程,解得A,B,C.从而得出等差数列{an}是常数列,结合题中条件得出关于p,q的方程即可求得求p,q的值;
(Ⅲ)当n=1时,得到B=2-A所以an+Sn=An+(2-A),当n≥1时,由题意得出数列{an-A}是公比为 的等比数列,下面对A进行分类讨论:①当A>1时②当0<A<1时.利用不等式的放缩即可得出M的取值范围.
的等比数列,下面对A进行分类讨论:①当A>1时②当0<A<1时.利用不等式的放缩即可得出M的取值范围.
解答:解:(Ⅰ)A=0时,an+Sn=B,
当n≥2时,由,{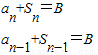 得,an-an-1+(Sn-Sn-1)=0
得,an-an-1+(Sn-Sn-1)=0
即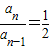 ,所以,数列{an}是等比数列.(4分)
,所以,数列{an}是等比数列.(4分)
(Ⅱ)设数列的公差为d,分别令n=1,2,3得:,
{ ,即,{
,即,{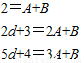 ,解得,{
,解得,{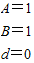 ,
,
即等差数列{an}是常数列,所以Sn=n;(7分)
又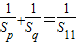 ,则
,则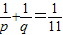 ,pq-11p-11q=0,(p-11)(q-11)=112,
,pq-11p-11q=0,(p-11)(q-11)=112,
因p<q,所以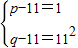 ,解得
,解得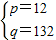 .(10分)
.(10分)
(Ⅲ)当n=1时,2=A+B,所以B=2-A
所以an+Sn=An+(2-A),
当n≥1时,由,{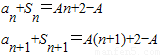
得an+1-an+(Sn+1-Sn)=A,
即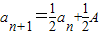
所以 ,又a1-A≠0
,又a1-A≠0
即数列{an-A}是公比为 的等比数列,
的等比数列,
所以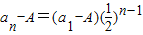 ,即
,即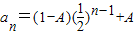 ,(12分)
,(12分)
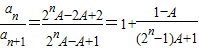 ,
,
①当A>1时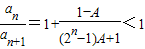
且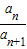 的值随n的增大而减小,
的值随n的增大而减小,
即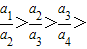 …,
…,
所以,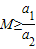 ,即M的取值范围是
,即M的取值范围是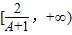 ;(14分)
;(14分)
②当0<A<1时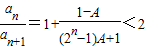
且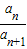 的值随n的增大而增大,
的值随n的增大而增大,
即 …<2,
…<2,
所以,M≥2,
综上即M的取值范围是[2,+∞).(16分)
点评:本小题主要考查等比关系的确定、数列与不等式的综合、不等式的性质等基础知识,考查运算求解能力,考查化归与转化思想.
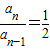 ,从而有数列{an}是等比数列;
,从而有数列{an}是等比数列;(Ⅱ)设数列的公差为d,分别令n=1,2,3得关于A,B,C的方程,解得A,B,C.从而得出等差数列{an}是常数列,结合题中条件得出关于p,q的方程即可求得求p,q的值;
(Ⅲ)当n=1时,得到B=2-A所以an+Sn=An+(2-A),当n≥1时,由题意得出数列{an-A}是公比为
 的等比数列,下面对A进行分类讨论:①当A>1时②当0<A<1时.利用不等式的放缩即可得出M的取值范围.
的等比数列,下面对A进行分类讨论:①当A>1时②当0<A<1时.利用不等式的放缩即可得出M的取值范围.解答:解:(Ⅰ)A=0时,an+Sn=B,
当n≥2时,由,{
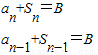 得,an-an-1+(Sn-Sn-1)=0
得,an-an-1+(Sn-Sn-1)=0即
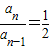 ,所以,数列{an}是等比数列.(4分)
,所以,数列{an}是等比数列.(4分)(Ⅱ)设数列的公差为d,分别令n=1,2,3得:,
{
 ,即,{
,即,{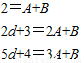 ,解得,{
,解得,{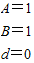 ,
,即等差数列{an}是常数列,所以Sn=n;(7分)
又
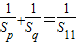 ,则
,则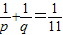 ,pq-11p-11q=0,(p-11)(q-11)=112,
,pq-11p-11q=0,(p-11)(q-11)=112,因p<q,所以
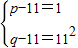 ,解得
,解得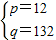 .(10分)
.(10分)(Ⅲ)当n=1时,2=A+B,所以B=2-A
所以an+Sn=An+(2-A),
当n≥1时,由,{
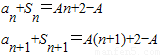
得an+1-an+(Sn+1-Sn)=A,
即
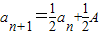
所以
 ,又a1-A≠0
,又a1-A≠0即数列{an-A}是公比为
 的等比数列,
的等比数列,所以
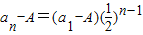 ,即
,即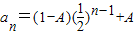 ,(12分)
,(12分)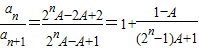 ,
,①当A>1时
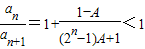
且
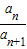 的值随n的增大而减小,
的值随n的增大而减小,即
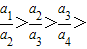 …,
…,所以,
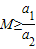 ,即M的取值范围是
,即M的取值范围是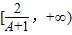 ;(14分)
;(14分)②当0<A<1时
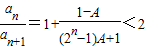
且
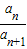 的值随n的增大而增大,
的值随n的增大而增大,即
 …<2,
…<2,所以,M≥2,
综上即M的取值范围是[2,+∞).(16分)
点评:本小题主要考查等比关系的确定、数列与不等式的综合、不等式的性质等基础知识,考查运算求解能力,考查化归与转化思想.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目