题目内容
已知数列{an}满足Sn=(1)求数列{an}的前n项的和;
(2)证明:![]() ≤
≤![]() <2.
<2.
解析:(1)由题意Sn=![]() an,得Sn+1=
an,得Sn+1=![]() an+1.
an+1.
两式相减得2an+1=(n+1)an+1-nan,即(n-1)an+1=nan.
所以(n+1)an+1=nan+2.
再相加2nan+1=nan+![]() ,即2an+1=an+an+2.
,即2an+1=an+an+2.
所以数列{an}是等差数列.
又∵a1=![]() a1,
a1,
∴a1=0.
又a2=1,∴an=n-1.
所以数列{an}的前n项的和为Sn=![]() an=
an=![]() .
.
(2)![]() =(1+
=(1+![]() )n
)n
=![]() .
.
∵![]() (r=1,2,…,n),
(r=1,2,…,n),
∴(1+![]() )n<1+
)n<1+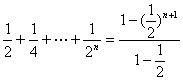
=2-(![]() )n<2
)n<2
而(1+![]() )n≥
)n≥![]() +
+![]() ·
·![]() ,
,
∴![]() <2.
<2.

练习册系列答案
相关题目