题目内容
若△ABC满足sinA=2sinC•cosB，则△ABC是
- A.等腰三角形
- B.直角三角形
- C.等腰直角三角形
- D.任意三角形
A
分析：由正弦定理可得cosB=
，再由余弦定理可得 cosB=
，由 
，
化简可得 b2=c2，故△ABC是等腰三角形．
解答：△ABC满足sinA=2sinC•cosB，由正弦定理可得 a=2c•cosB，∴cosB=．
再由余弦定理可得 cosB=，∴，化简可得 b2=c2，
故有b=c，故选A．
点评：本题考查正弦定理、余弦定理的应用，得到，是解题的关键．
分析：由正弦定理可得cosB=
，再由余弦定理可得 cosB=，由 ，化简可得 b2=c2，故△ABC是等腰三角形．
解答：△ABC满足sinA=2sinC•cosB，由正弦定理可得 a=2c•cosB，∴cosB=
．再由余弦定理可得 cosB=
，∴，化简可得 b2=c2，故有b=c，故选A．
点评：本题考查正弦定理、余弦定理的应用，得到
，是解题的关键． 
练习册系列答案
口算题天天练系列答案
相关题目
）-
cos（ωx+
）的值；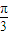
）-
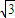cos（ωx+
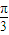）（ω＞0）的最小正周期为π．
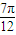）的值；