题目内容
【题目】已知函数![]() .
.
(1)若![]() ,且
,且![]() 在
在![]() 上的最大值为
上的最大值为![]() ,最小值为-2,试求
,最小值为-2,试求![]() 的值;
的值;
(2)若![]() ,
,![]() ,且
,且![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.(用
的取值范围.(用![]() 来表示)
来表示)
【答案】(1)![]() ;(2)
;(2)![]() 时,
时,![]() ;
;![]() 时,
时,![]() ;
;
![]() 时,
时,![]() .
.
【解析】
试题分析:(1)这是二次函数,最大值、最小值与对称轴有关,其对称轴为![]() >0,因此只要分
>0,因此只要分![]() 及
及![]() 两类分别求解;(2)
两类分别求解;(2)![]() ,
,![]() 即
即![]() ,因此此最大值小于等于2,最小值大于等于-2,而
,因此此最大值小于等于2,最小值大于等于-2,而![]() 在
在![]() 时取最小值,因此分
时取最小值,因此分![]() ,
,![]() ,
,![]() 三类进行讨论求解.
三类进行讨论求解.
试题解析:(1)抛物线的对称轴为![]() ,
,
①当![]() 时,即
时,即![]() 时,
时,
当![]() 时,
时,![]() ,
,
![]() ,
,
∴ ,
,
∴![]() .
.
②当![]() 时,即
时,即![]() 时,
时,
![]() 在
在![]() 上为增函数,
上为增函数,![]() 与
与![]() 矛盾,无解,
矛盾,无解,
综合得:![]() .
.
(2)![]() 对任意
对任意![]() 恒成立,即
恒成立,即![]() 对任意
对任意![]() 恒成立,
恒成立,
即![]() 对任意
对任意![]() 恒成立,
恒成立,
令![]() ,则
,则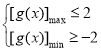 ,
,
∵![]() ,∴
,∴![]() ,
,
(ⅰ)![]() ,即
,即![]() 时,
时,![]() 在
在![]() 单调递减,此时
单调递减,此时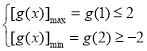 ,
,
即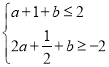 ,得
,得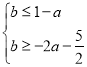 ,此时
,此时![]() ,∴
,∴![]()
∴![]() .
.
(ⅱ)![]() ,即
,即![]() 时,
时,![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
此时,![]() ,
,
只要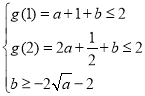
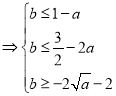 ,
,![]()
当![]() 时,
时,![]() ,
,![]()
当![]() 时,
时,![]() ,
,![]() .
.
综上得:①![]() 时,
时,![]() ;
;
②![]() 时,
时,![]() ;
;
③![]() 时,
时,![]() .
.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
