题目内容
设函数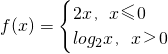 ,若关于f2(x)-af(x)=0的方程恰有三个不同的实数解,则实数a的取值范围为________.
,若关于f2(x)-af(x)=0的方程恰有三个不同的实数解,则实数a的取值范围为________.
{a|a>0}
分析:设f(x)=t,先将解已知方程问题转化为解方程f(x)=0和f(x)=a共有三个根问题,再画出函数f(x)的图象,数形结合即可得a的范围
解答:设f(x)=t,则方程t2-at=0有两个根0,a;
函数f(x)的图象如图 ,
,
f(x)=0有两个根0,1
要使关于f2(x)-af(x)=0的方程恰有三个不同的实数解
需f(x)=a有且只有一个根
数形结合可知需a>0
故答案为 a>0
点评:本题主要考查了换元法解方程的方法,利用函数图象数形结合解方程的方法和技巧,转化化归的思想方法,属基础题
分析:设f(x)=t,先将解已知方程问题转化为解方程f(x)=0和f(x)=a共有三个根问题,再画出函数f(x)的图象,数形结合即可得a的范围
解答:设f(x)=t,则方程t2-at=0有两个根0,a;
函数f(x)的图象如图
 ,
,f(x)=0有两个根0,1
要使关于f2(x)-af(x)=0的方程恰有三个不同的实数解
需f(x)=a有且只有一个根
数形结合可知需a>0
故答案为 a>0
点评:本题主要考查了换元法解方程的方法,利用函数图象数形结合解方程的方法和技巧,转化化归的思想方法,属基础题

练习册系列答案
相关题目
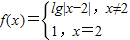 ,若关于x的方程f2(x)+bf(x)+c=0恰有5个不同的实数解x1、x2、x3、x4、x5则f(x1+x2+x3+x4+x5)等于 .
,若关于x的方程f2(x)+bf(x)+c=0恰有5个不同的实数解x1、x2、x3、x4、x5则f(x1+x2+x3+x4+x5)等于 .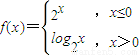 ,若关于x的方程f2(x)-af(x)=0恰有三个不同的实数解,则实数a的取值范围为 .
,若关于x的方程f2(x)-af(x)=0恰有三个不同的实数解,则实数a的取值范围为 .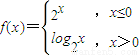 ,若关于x的方程f2(x)-af(x)=0恰有三个不同的实数解,则实数a的取值范围为 .
,若关于x的方程f2(x)-af(x)=0恰有三个不同的实数解,则实数a的取值范围为 .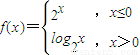 ,若关于x的方程f2(x)-af(x)=0恰有三个不同的实数解,则实数a的取值范围为 .
,若关于x的方程f2(x)-af(x)=0恰有三个不同的实数解,则实数a的取值范围为 .