Question

（本小题满分12分）

已知直四棱柱ABCD—A₁B₁C₁D₁的底面是菱形，且∠DAB=60°，AD=AA₁，F为棱BB₁的中点，M为线段AC₁的中点。

   （1）求证：直线MF∥平面ABCD；

   （2）求证：平面AFC₁⊥平面ACC₁A₁；

   （3）求平面AFC₁与平面ABCD所成二面角的大小。

Answer 1

（本小题满分12分）解法一：

   （1）延长C₁F交CB的延长线于点N，连接AN。因为F是BB₁的中点，

       所以F为C₁N的中点，B为CN的中点。

       又M是线段AC₁的中点，故MF∥AN。

       又MF平面ABCD，AN平面ABCD。

       ∴MF∥平面ABCD。 

   （2）证明：连BD，由直四棱柱ABCD—A₁B₁C₁D₁

       可知A₁A⊥平面ABCD，

       又∵BD平面ABCD， ∴A₁A⊥BD。

       ∵四边形ABCD为菱形，∴AC⊥BD。

       又∵AC∩A₁A=A，AC，A₁A平面ACC₁A₁。

       ∴BD⊥平面ACC₁A₁。       

       在四边形DANB中，DA∥BN且DA=BN，所以四边形DANB为平行四边形

       故NA∥BD，∴NA⊥平面ACC₁A₁，又因为NA平面AFC₁

       ∴平面AFC₁⊥ACC₁A₁

   （3）由（2）知BD⊥ACC₁A₁，又AC₁ACC₁A₁，

       ∴BD⊥AC₁，∴BD∥NA，∴AC₁⊥NA。

       又由BD⊥AC可知NA⊥AC，

       ∴∠C₁AC就是平面AFC₁与平面ABCD所成二面角的平面角或补角。

       在Rt△C₁AC中，，   

       故∠C₁AC=30°

       ∴平面AFC₁与平面ABCD所成二面角的大小为30°或150°

       解法二：

       设AC∩BD=0，因为M、O分别为C₁A、CA的中点，所以，MO∥C₁C，

       又由直四棱柱知C₁C⊥平面ABCD，所以MO⊥平面ABCD。

       在棱形ABCD中，BD⊥AC，所以，OB、OC、OM两两垂直。

       故可以O为原点，OB、OC、OM所在直线分别为x轴、y轴、z轴如图建立空间直角坐

       标系

       若设|OB|=1，则B（1，0，0），B₁（1，0，2），

       A（0，，0），C（0，，0），C₁（0，，2）。          

   （1）由F、M分别为B₁B、C₁A的中点可知：F（1，0，1），

       M（0，0，1），所以（1，0，0）=

       又不共线，所以，MF∥OB。

       ∵MF平面ABCD，OB平面ABCD，

       ∴MF∥平面ABCD。 

   （2）（1，0，0）为平面ACC₁A₁的法向量。

    设为平面AFC₁的一个法向量

       则

       由得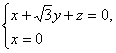

       令y=1，得z=，此时                  

       由于，所以，平面AFC₁⊥平面ACC₁A₁。      

   （3）为平面ABCD的法向量，设平面AFC₁与平面ABCD所成的二面角

       的大小为，

       则

       所以=30°或150°。

       即平面AFC₁与平面ABCD所成二面角的大小为30°或150°。