题目内容
数列{an}中，a1=1，对于所有的n≥2，n∈N都有a1•a2•a3•…•an=n2，则a3+a5等于
- A.
- B.
- C.
- D.
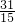
A
分析：由n≥2，n∈N时a1•a2•a3•…•an=n2得当n≥3时，a1•a2•a3••an-1=（n-1）2．然后两式相除an=（
）2，即可得a3=
，a5=从而求得a3+a5=．
解答：当n≥2时，a1•a2•a3••an=n2．
当n≥3时，a1•a2•a3••an-1=（n-1）2．
两式相除an=（）2，
∴a3=，a5=．∴a3+a5=．
故选A
点评：本题考查了数列的概念及简单表示法，培养学生观察、分析、归纳、推理的能力，提高学生分析问题和解决问题的能力．是基础题．
分析：由n≥2，n∈N时a1•a2•a3•…•an=n2得当n≥3时，a1•a2•a3••an-1=（n-1）2．然后两式相除an=（
）2，即可得a3=，a5=从而求得a3+a5=．解答：当n≥2时，a1•a2•a3••an=n2．
当n≥3时，a1•a2•a3••an-1=（n-1）2．
两式相除an=（
）2，∴a3=
，a5=．∴a3+a5=．故选A
点评：本题考查了数列的概念及简单表示法，培养学生观察、分析、归纳、推理的能力，提高学生分析问题和解决问题的能力．是基础题．
练习册系列答案
相关题目
数列{an}中，a1=
，an+an+1=
，n∈N*，则
（a1+a2+…+an）等于（ ）
| 1 |
| 5 |
| 6 |
| 5n+1 |
| lim |
| n→∞ |
A、
| ||
B、
| ||
C、
| ||
D、
|