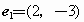题目内容
设 ,则与
,则与 平行的单位向量的坐标为 ,同时垂直于
平行的单位向量的坐标为 ,同时垂直于 的单位向量
的单位向量 = .
= .
【答案】分析:设出满足条件的向量的坐标,然后根据两个向量平行,则存在实数使 ,两个向量垂直则向量的数量积为0,单位向量的模为1,构造方程(组),解方程(组)即可求出满足条件的向量的坐标.
,两个向量垂直则向量的数量积为0,单位向量的模为1,构造方程(组),解方程(组)即可求出满足条件的向量的坐标.
解答:解:①设与 平行的单位向量的坐标为
平行的单位向量的坐标为 则
则
 =(2μ,6μ,-3μ)
=(2μ,6μ,-3μ)
且| |=1=
|=1=
解得
∴ =
= 或
或 =
=
②同时垂直于 的单位向量
的单位向量 =(x,y,z)
=(x,y,z)
则
即
解得: 或
或
∴ =
= 或
或 =
=
故答案为: 或
或 ;
; 或
或
点评:本题考查的知识点是向量语文表述线线的垂直、平行关系,其中根据两个向量平行,则存在实数使 ,两个向量垂直则向量的数量积为0,单位向量的模为1,构造方程(组),是解答本题的关键.
,两个向量垂直则向量的数量积为0,单位向量的模为1,构造方程(组),是解答本题的关键.
 ,两个向量垂直则向量的数量积为0,单位向量的模为1,构造方程(组),解方程(组)即可求出满足条件的向量的坐标.
,两个向量垂直则向量的数量积为0,单位向量的模为1,构造方程(组),解方程(组)即可求出满足条件的向量的坐标.解答:解:①设与
 平行的单位向量的坐标为
平行的单位向量的坐标为 则
则 =(2μ,6μ,-3μ)
=(2μ,6μ,-3μ)且|
 |=1=
|=1=
解得

∴
 =
= 或
或 =
=
②同时垂直于
 的单位向量
的单位向量 =(x,y,z)
=(x,y,z)则

即

解得:
 或
或
∴
 =
= 或
或 =
=
故答案为:
 或
或 ;
; 或
或
点评:本题考查的知识点是向量语文表述线线的垂直、平行关系,其中根据两个向量平行,则存在实数使
 ,两个向量垂直则向量的数量积为0,单位向量的模为1,构造方程(组),是解答本题的关键.
,两个向量垂直则向量的数量积为0,单位向量的模为1,构造方程(组),是解答本题的关键. 
练习册系列答案
相关题目
选择题:
(1)
如果a,b是两个单位向量,那么下列四个结论中正确的是[
]|
(A)a =b |
(B)a ·b=1 |
|
(C) |
(D) |
(2)
对于任意向量a、b,下列命题中正确的是[
](A)
若a,b满足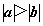 ,且a与b同向,则a>b
,且a与b同向,则a>b
(B)
(C)
(D)
(3)在四边形ABCD中,若 ,则
,则
[
]|
(A)ABCD 是矩形 |
(B)ABCD 是菱形 |
|
(C)ABCD 是正方形 |
(D)ABCD 是平行四边形 |
(4)
设a是非零向量,λ是非零实数,下列结论中正确的是[
]|
(A)a 与-λa的方向相反 |
(B) |
|
(C)a 与 的方向相同 的方向相同 |
(D) |
(5)
设M是□ABCD的对角线的交点,O为任意一点,则 等于
等于
[
]|
(A) |
(B)2 |
(C)3 |
(D)4 |
(6)
下列各组向量中,可以作为基底的是[
](A)
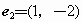
(B)
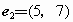
(C)
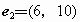
(D)