题目内容
已知函数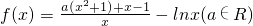 .
.
(1)当 时,讨论f(x)的单调性;
时,讨论f(x)的单调性;
(2)设g(x)=x2-2bx+4,当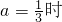 ,若对任意x1∈(0,2),存在x2∈[1,2],使f(x1)+g(x2)≤0,求实数b的取值范围.
,若对任意x1∈(0,2),存在x2∈[1,2],使f(x1)+g(x2)≤0,求实数b的取值范围.
解:(1)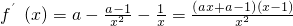 .(2分)
.(2分)
①当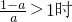 ,即
,即 时,此时f(x)的单调性如下:
时,此时f(x)的单调性如下:
(4分)
②当a=0时,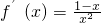 ,当0<x<1时f(x)递增;
,当0<x<1时f(x)递增;
当x>1时,f(x)递减;(5分)
③当a<0时,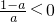 ,当0<x<1时f(x)递增;
,当0<x<1时f(x)递增;
当x>1时,f(x)递减;(6分)
综上,当a≤0时,f(x)在(0,1)上是增函数,在(1,+∞)上是减函数;
当 时,f(x)在(0,1),(
时,f(x)在(0,1),(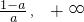 )上是增函数,
)上是增函数,
在(1,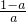 )上是减函数.(7分)
)上是减函数.(7分)
(2)由(1)知,当 时,f(x)在(0,1)上是增函数,在(1,2)上是减函数.
时,f(x)在(0,1)上是增函数,在(1,2)上是减函数.
于是x1∈(0,2)时, .(8分)
.(8分)
从而存在x2∈[1,2],
使g(x2)=
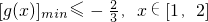 (10分)
(10分)
考察g(x)=x2-2bx+4=(x-b)2+4-b2,x∈[1,2]的最小值.
①当b≤1时,g(x)在[1,2]上递增,[g(x)]min= (舍去)..(11分)
(舍去)..(11分)
②当b≥2时,,g(x)在[1,2]上递减,

∴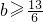 ..(12分)
..(12分)
③当1<b<2时,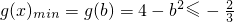 ,无解.(13分)
,无解.(13分)
综上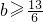 (14分)
(14分)
分析:(1)先对函数y=f(x)进行求导,然后令导函数大于0(或小于0)求出x的范围,根据f′(x)>0求得的区间是单调增区间,f′(x)<0求得的区间是单调减区间,即可得到答案.
(2)由(1)知,当 时,f(x)在(0,1)上是增函数,在(1,2)上是减函数.于是x1∈(0,2)时,
时,f(x)在(0,1)上是增函数,在(1,2)上是减函数.于是x1∈(0,2)时, 从而存在x2∈[1,2],使g(x2)=x22-2bx2+4,且
从而存在x2∈[1,2],使g(x2)=x22-2bx2+4,且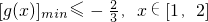 下面考查g(x)=x2-2bx+4=(x-b)2+4-b2,x∈[1,2]的最小值.对字母b进行分类讨论:①当b≤1时,②当b≥2时,③当1<b<2时,即可求得实数b的取值范围.
下面考查g(x)=x2-2bx+4=(x-b)2+4-b2,x∈[1,2]的最小值.对字母b进行分类讨论:①当b≤1时,②当b≥2时,③当1<b<2时,即可求得实数b的取值范围.
点评:本题主要考查导数在最大值、最小值问题中的应用及导函数的正负与原函数的单调性之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.属于基础题.
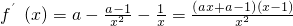 .(2分)
.(2分)①当
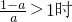 ,即
,即 时,此时f(x)的单调性如下:
时,此时f(x)的单调性如下:| x | (0,1) | 1 | (1,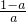 ) ) | 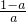 | (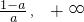 ) ) |
| f′(x) | + | 0 | _ | 0 | + |
| f(x) | 增 | 减 | 增 |
②当a=0时,
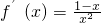 ,当0<x<1时f(x)递增;
,当0<x<1时f(x)递增;当x>1时,f(x)递减;(5分)
③当a<0时,
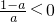 ,当0<x<1时f(x)递增;
,当0<x<1时f(x)递增;当x>1时,f(x)递减;(6分)
综上,当a≤0时,f(x)在(0,1)上是增函数,在(1,+∞)上是减函数;
当
 时,f(x)在(0,1),(
时,f(x)在(0,1),(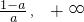 )上是增函数,
)上是增函数,在(1,
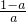 )上是减函数.(7分)
)上是减函数.(7分)(2)由(1)知,当
 时,f(x)在(0,1)上是增函数,在(1,2)上是减函数.
时,f(x)在(0,1)上是增函数,在(1,2)上是减函数.于是x1∈(0,2)时,
 .(8分)
.(8分)从而存在x2∈[1,2],
使g(x2)=

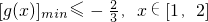 (10分)
(10分)考察g(x)=x2-2bx+4=(x-b)2+4-b2,x∈[1,2]的最小值.
①当b≤1时,g(x)在[1,2]上递增,[g(x)]min=
 (舍去)..(11分)
(舍去)..(11分)②当b≥2时,,g(x)在[1,2]上递减,


∴
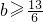 ..(12分)
..(12分)③当1<b<2时,
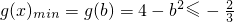 ,无解.(13分)
,无解.(13分)综上
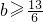 (14分)
(14分)分析:(1)先对函数y=f(x)进行求导,然后令导函数大于0(或小于0)求出x的范围,根据f′(x)>0求得的区间是单调增区间,f′(x)<0求得的区间是单调减区间,即可得到答案.
(2)由(1)知,当
 时,f(x)在(0,1)上是增函数,在(1,2)上是减函数.于是x1∈(0,2)时,
时,f(x)在(0,1)上是增函数,在(1,2)上是减函数.于是x1∈(0,2)时, 从而存在x2∈[1,2],使g(x2)=x22-2bx2+4,且
从而存在x2∈[1,2],使g(x2)=x22-2bx2+4,且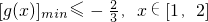 下面考查g(x)=x2-2bx+4=(x-b)2+4-b2,x∈[1,2]的最小值.对字母b进行分类讨论:①当b≤1时,②当b≥2时,③当1<b<2时,即可求得实数b的取值范围.
下面考查g(x)=x2-2bx+4=(x-b)2+4-b2,x∈[1,2]的最小值.对字母b进行分类讨论:①当b≤1时,②当b≥2时,③当1<b<2时,即可求得实数b的取值范围.点评:本题主要考查导数在最大值、最小值问题中的应用及导函数的正负与原函数的单调性之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .
.  时,求函数
时,求函数 的定义域;
的定义域; 的不等式
的不等式 的解集是
的解集是 ,求
,求 的取值范围.
的取值范围.
 。
。 时,判断
时,判断 的单调性;
的单调性; 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围;
的取值范围; .
. 时,求满足
时,求满足 的
的 的取值范围;
的取值范围; 的定义域为R,又是奇函数,求
的定义域为R,又是奇函数,求 .
. 时,如果函数
时,如果函数 仅有一个零点,求实数
仅有一个零点,求实数 的取值范围;
的取值范围; 时,试比较
时,试比较 与
与 的大小;
的大小; (
( ).
).