题目内容
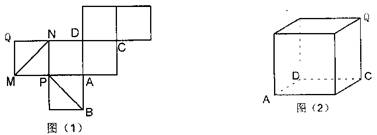
如图(1)是一正方体的表面展开图,MN和PB是两条对角线,请在图(2)的正方体中将MN和PB画出来,并就这个正方体解决下面问题.(1)求证:MN∥平面PBD;
(2)求证:AQ⊥平面PBD;
(3)求二面角P-DB-M的大小.

【答案】分析:(1)先将展开图进行还原,欲证MN∥平面PBD,根据直线与平面平行的判定定理可知只需证MN与平面PBD内一直线平行,根据四边形NDBM为平行四边形,则MN∥DB,而BD⊆平面PBD,MN?平面PBD,满足定理所需条件;
(2)欲证AQ⊥面PDB,根据直线与平面垂直的判定定理可知只需证AQ与面PDB内两相交直线垂直,根据线面垂直的性质可知AQ⊥BD,同理可得AQ⊥PB,BD∩PD=B,满足定理所需条件;
(3)分别取DB、MN中点E、F连接PE、EF、PF,根据二面角平面角的定义可知∠PEF为二面角P-DB-M为平面角,在直角三角形EFP中求出此角即可.
解答:解:M、N、Q、B的位置如图示.
(1)∵ND∥MB且ND=MB
∴四边形NDBM为平行四边形
∴MN∥DB(3分)
∴BD⊆平面PBD,MN?平面PBD
∴MN∥平面PBD(4分)
(2)∵QC⊥平面ABCD,BD?平面ABCD,
∴BD⊥QC(5分)
又∵BD⊥AC,
∴BD⊥平面AQC(6分)
∵AQ?面AQC
∴AQ⊥BD,同理可得AQ⊥PB,
 ∵BD∩PB=B
∵BD∩PB=B
∴AQ⊥面PDB(8分)
(3)解:分别取DB、MN中点E、F连接PE、EF、PF(9分)
∵在正方体中,PB=PB
∴PE⊥DB(10分)
∵四边形NDBM为矩形
∴EF⊥DB
∴∠PEF为二面角P-DB-M为平面角(11分)
∵EF⊥平面PMN
∴EF⊥PF
设正方体的棱长为a,则在直角三角形EFP中
∵EF=a,PF=
∴tan∠PEF=
∠PEF=arctan (13分)
(13分)
点评:本题主要考查直线与平面平行的判定,以及直线与平面垂直的判定和二面角的度量,二面角的求解在最近两年高考中频繁出现,值得重视.
(2)欲证AQ⊥面PDB,根据直线与平面垂直的判定定理可知只需证AQ与面PDB内两相交直线垂直,根据线面垂直的性质可知AQ⊥BD,同理可得AQ⊥PB,BD∩PD=B,满足定理所需条件;
(3)分别取DB、MN中点E、F连接PE、EF、PF,根据二面角平面角的定义可知∠PEF为二面角P-DB-M为平面角,在直角三角形EFP中求出此角即可.
解答:解:M、N、Q、B的位置如图示.
(1)∵ND∥MB且ND=MB
∴四边形NDBM为平行四边形

∴MN∥DB(3分)
∴BD⊆平面PBD,MN?平面PBD
∴MN∥平面PBD(4分)
(2)∵QC⊥平面ABCD,BD?平面ABCD,
∴BD⊥QC(5分)
又∵BD⊥AC,
∴BD⊥平面AQC(6分)
∵AQ?面AQC
∴AQ⊥BD,同理可得AQ⊥PB,
 ∵BD∩PB=B
∵BD∩PB=B∴AQ⊥面PDB(8分)
(3)解:分别取DB、MN中点E、F连接PE、EF、PF(9分)
∵在正方体中,PB=PB
∴PE⊥DB(10分)
∵四边形NDBM为矩形
∴EF⊥DB
∴∠PEF为二面角P-DB-M为平面角(11分)
∵EF⊥平面PMN
∴EF⊥PF
设正方体的棱长为a,则在直角三角形EFP中
∵EF=a,PF=

∴tan∠PEF=

∠PEF=arctan
 (13分)
(13分)点评:本题主要考查直线与平面平行的判定,以及直线与平面垂直的判定和二面角的度量,二面角的求解在最近两年高考中频繁出现,值得重视.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 如图(1)是一正方体的表面展开图,MN和PB是两条对角线,请在图(2)的正方体中将MN和PB画出来,并就这个正方体解决下面问题.
如图(1)是一正方体的表面展开图,MN和PB是两条对角线,请在图(2)的正方体中将MN和PB画出来,并就这个正方体解决下面问题. (2007•揭阳二模)如图(1)是一正方体的表面展开图,MN和PB是两条面对角线,请在图(2)的正方体中将MN和PB画出来,并就这个正方体解决下面问题.
(2007•揭阳二模)如图(1)是一正方体的表面展开图,MN和PB是两条面对角线,请在图(2)的正方体中将MN和PB画出来,并就这个正方体解决下面问题.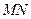 和
和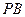 是两条面对角线,请在图(2)的正方体中将
是两条面对角线,请在图(2)的正方体中将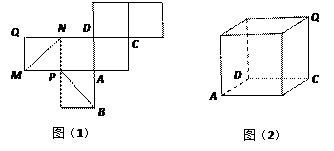
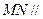 平面
平面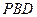 ;
;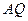 ⊥平面
⊥平面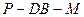 的大小.
的大小.