题目内容
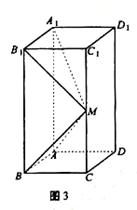
如图所示,在长方体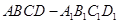 中,
中,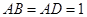 ,
,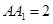 ,
,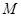 是棱
是棱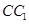 上一点,
上一点,
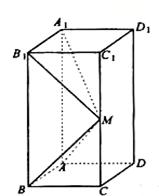
(1)若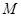 为CC1的中点,求异面直线A1M和C1D1所成的角的正切值;
为CC1的中点,求异面直线A1M和C1D1所成的角的正切值;
(2)是否存在这样的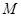 ,使得平面ABM⊥平面A1B1M,若存在,求出
,使得平面ABM⊥平面A1B1M,若存在,求出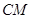 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
【答案】
(1)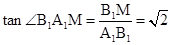 。(2)
。(2)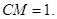
【解析】
试题分析:(1)由于C1D1∥B1A1故根据异面直线所成角的定义可知∠MA1B1为异面直线A1M和C1D1所成的角然后在解三角形MA1B1求出∠MA1B1的正切值即可.
(Ⅱ)可根据题中条件设出点M的坐标,然后根据面面垂直,计算得出A1B1⊥BM,BM⊥B1M然后再根据面面垂直的判定定理即可得证.
解:(1)∵C1D1∥A1B1
∴∠B1A1M即为直线A1M和C1D1所成的角
∴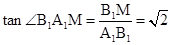 。
。
(2)建立坐标系: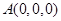 ,
,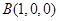 ,
,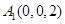 ,
,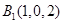 ,
,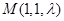
在平面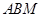 上选择向量
上选择向量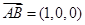 ,
,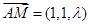 ,设法向量
,设法向量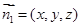
由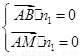 ,解得
,解得 ,取
,取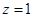 ,得
,得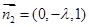
在平面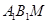 上选择向量
上选择向量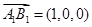 ,
,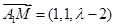 ,设法向量
,设法向量
由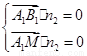 ,解得
,解得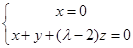 ,取
,取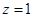 ,得
,得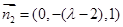 ,
,
由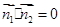 ,
,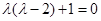 ,解得
,解得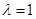 ,所以
,所以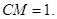
考点:本试题主要考查了考察异面直线所成角的定义以及面面垂直的证明,属常考题型,较难.
点评:解题的关键是要掌握异面直线所成角的定义(即将异面直线转化为相交直线所成的角)和面面垂直的判定定理。

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
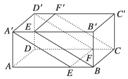

 中,AB=AD=1,AA1=2,M是棱CC1的中点
中,AB=AD=1,AA1=2,M是棱CC1的中点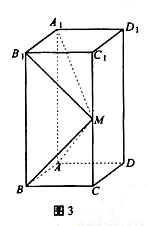
 中,AB=AD=1,AA1=2,M是棱CC1的中点
中,AB=AD=1,AA1=2,M是棱CC1的中点