题目内容
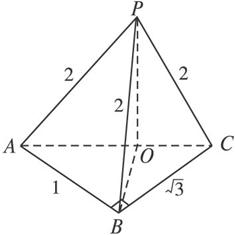
(文13)三棱锥P—ABC中,PA=PB=PC=2,AB⊥BC,AB=1,BC=3,则点P到平面ABC的距离为____________.
解析:∵PA=PB=PC,∴P在面ABC上的射影O为△ABC的外心.
又∠ABC=90°,
∴O为AC的中点.
∴P到面ABC的距离为PO=
.
答案:
练习册系列答案
教材全解字词句篇系列答案
相关题目
教材全解字词句篇系列答案题目内容
(文13)三棱锥P—ABC中,PA=PB=PC=2,AB⊥BC,AB=1,BC=3,则点P到平面ABC的距离为____________.
解析:∵PA=PB=PC,∴P在面ABC上的射影O为△ABC的外心.
又∠ABC=90°,
∴O为AC的中点.
∴P到面ABC的距离为PO=.
答案:
教材全解字词句篇系列答案